Question

If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then the triangles on both sides of the perpendicular are similar to the whole triangle and also to each other.

Answer 1

Hint: First we need to draw the diagram using the given condition in the question and we have to prove :
\[
  \Delta ADB \sim \Delta ABC \\
  {\text{ }}\Delta BDC \sim \Delta ABC \\
  {\text{ }}\Delta {\text{ }}ADB \sim \Delta BDC \\
 \]
Using the properties of similar triangles.

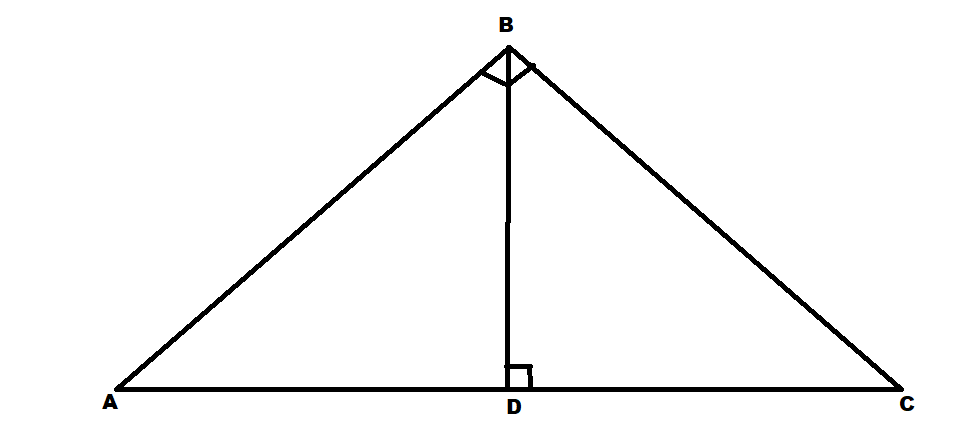
Complete step by step answer:
We are given that \[\Delta ABC\] is right angled at B and a perpendicular is drawn from B to hypotenuse AC at D.
So we need to prove that
\[
  \Delta ADB \sim \Delta ABC \\
  {\text{ }}\Delta BDC \sim \Delta ABC \\
  {\text{ }}\Delta {\text{ }}ADB \sim \Delta BDC \\
 \]
Firstly we will consider \[\Delta ADB\] and \[\Delta ABC\]

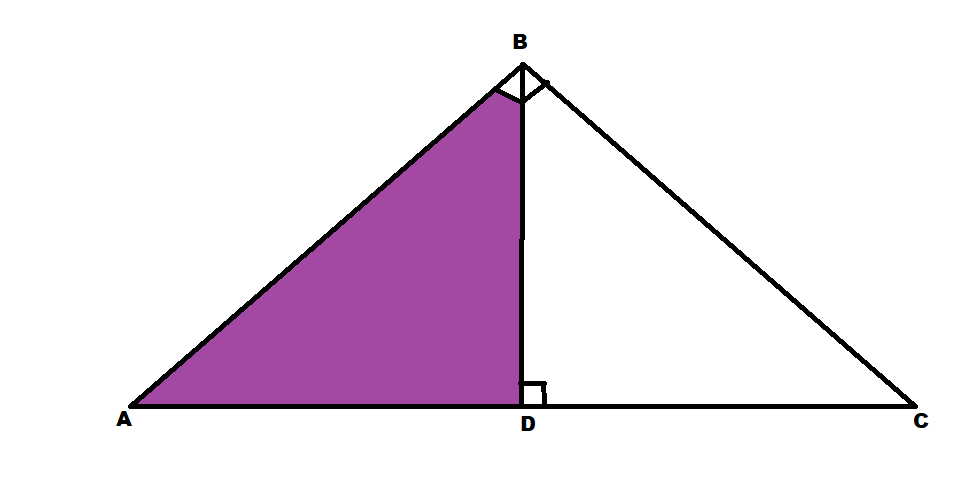
\[\angle ADB = \angle ABC\] (\[{90^ \circ }\] angle)
\[\angle A = \angle A\] (common angle)
Since two angles are equal therefore the third corresponding angles of the triangles will be equal
Therefore,
\[\angle ABD = \angle ACB\]
Hence \[\Delta ADB \sim \Delta ABC\] by AAA criterion. …………(1)
Now, we will consider \[\Delta BDC\] and \[\Delta ABC\]

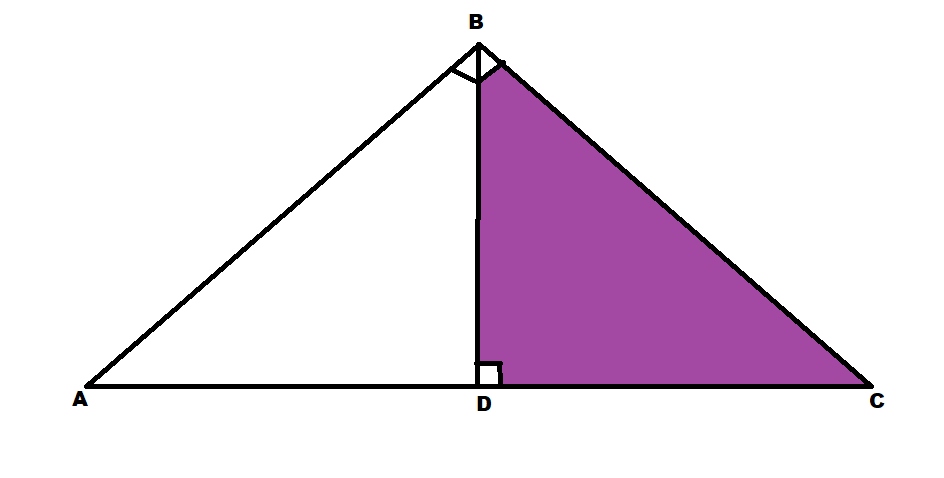
\[\angle BDC = \angle ABC\] (\[{90^ \circ }\] angle)
\[\angle C = \angle C\] (common angle)
Since two angles are equal therefore the third corresponding angles of the triangles will be equal
Therefore,
\[\angle CBD = \angle CAB\]
Hence \[\Delta BDC \sim \Delta ABC\] by AAA criterion. …………………(2)
Since from (1) and (2)
\[\Delta ADB \sim \Delta ABC\] and \[\Delta BDC \sim \Delta ABC\]

Therefore, \[{\text{ }}\Delta {\text{ }}ADB \sim \Delta BDC\]. Hence proved.

Note:
The similarity of triangles has several criterions:
AAA (angle angle angle) criterion in which the angles of the similar triangles are equal
SAS(side angle side) criterion in which two sides of similar triangles are in the same ratio and the angle between them is equal.
ASA(angle side angle) criterion in which two angles of the similar triangles are equal and angle between them is equal.
SSS(side side side) criterion in which the ratio of the sides of the similar triangles are equal.