Question

If a pair of opposite angles of a quadrilateral are supplementary, the quadrilateral is a
A. Cyclic
B. Parallelogram
C. Rectangle
D. Rhombus

Answer 1

Hint: In this question, we have to prove that if a pair of opposite angles of a quadrilateral are supplementary, then all it’s vertices will lie on a circle. By assuming that any 3 non collinear forms a circle such that the point does not lie on the circle.

Complete step-by-step answer:

In this question, the most possible answer is either cyclic or rectangle because parallelogram and rhombus have a property that they have a pair of consecutive angle’s sum as 180˚. And pairs of opposite angles are equal. So, they are possibly the wrong answer. Now, if we consider a rectangle, it has a sum of pairs of opposite angles as 180˚ because all corner angles are 90˚.
In the question, we have been asked to find the quadrilateral in which the sum of pairs of opposite angles is supplementary, and the rectangle is a specific case of this property. Because, if we take a pair of opposite angles as 70˚ and 110˚, then it will not form a rectangle but will definitely have a sum of pairs of opposite angles as 180˚. So, rectangle is also the wrong answer.
Now we will check for cyclic quadrilateral by contradiction. So, let us assume that, out of 4 points of quadrilateral, 3 of them lie on a circle and the 4th point lies somewhere outside the circle. So, we can represent it diagrammatically as follows.

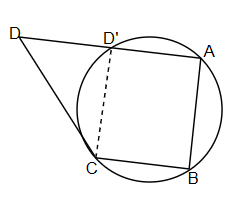
Here, ABCD is a quadrilateral and a circle passes through ABC and intersect AD at D’. Now, we can see that ABCD’ forms a cyclic quadrilateral. And cyclic quadrilateral has a property that sum of opposite pair of angles is 180˚. So, we can write, $\angle CBA+\angle AD'C=180{}^\circ .........(i)$. But we are given that $\angle CBA+\angle ADC=180{}^\circ .........(ii)$. Now, we will equate equation (i) and equation (ii). So, we will get,
$\angle CBA+\angle AD'C=\angle CBA+\angle ADC$. And after cancelling the same terms, we can write it as, $\angle AD'C=\angle ADC$. Which implies that D’ and D are the same point but we assumed that they are different. From this we can conclude that D’ and D coincide. That means ABCD is a cyclic quadrilateral.
Hence, option (A) is the correct answer.

Note: In this quadrilateral, we can say that if a pair of opposite angles are supplementary then the quadrilateral is a cyclic quadrilateral because, cyclic quadrilateral has a property that its opposite angles are a sum of 180˚.