Question

If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on the circle (i.e. they are concyclic)

Answer 1

Hint: Let us name the line segment as AB and take two other points on the same side of the line i.e. C & D. Now, draw a circle joining A, B & C because A, B & C are three non-collinear points. Let us assume that the point D does not lie on the circle and let the circle intersect AD at a point D’. Now to prove the points A, B, C & D are concyclic we are going to show that the points D and D’ coincide with each other which can be done using the property of the exterior angle of a triangle.

Complete step-by-step answer:

Let us name the line segment as AB. Now, we are going to mark two points on the same side of the line segment as C & D. The below figure is demonstrating what we have just said.

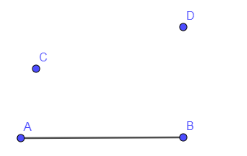
As you can see from the above figure that the points A, B & C are non – collinear so we can draw a circle joining these three points and the line joining A & D intersecting the circle at the point D’. The below diagram is showing a circle passing through the points A, B, C and AD is intersecting the circle at D’.

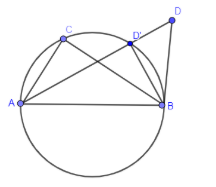
In the above figure, we know that the angles subtended on the same side of the circle by a line segment are equal so we can say that,
 $\angle ACB=\angle AD'B$………… Eq. (1)
It is given that:
 $\angle ACD=\angle ADB$………… Eq. (2)
We can see from the above eq. (1) and eq. (2) that:
$\angle AD'B=\angle ADB$………. Eq. (3)
Now, considering triangle BD’D. We know that an exterior angle of a triangle is equal to the two interior opposite angles so applying this property on $\Delta BD'D$ we get,
$\angle AD'B=\angle D'BD+\angle BDD'$
In the above equation, we can write $\angle AD'B=\angle ADB$ and we can also write $\angle D'BD=\angle ADB$ so substituting these angles in the above equation we get,
$\angle ADB=\angle D'BD+\angle ADB$
From the above equation, we can see that $\angle ADB$ will be cancelled out from both the sides of the above equation.
$\angle D'BD=0$
We have shown that $\angle D'BD=0$, it means the line BD is overlapped with the line BD’. Hence, point D’ is coinciding with the point D.
Thus, the assumption that we have taken that the point D and D’ are not coinciding with each other is wrong.
The above discussion is implying that A, B, C & D are concyclic.

Note: You might think why we have proved $\angle D'BD=0$ because we have to show that the point D and D’ are coinciding and to show this the only way is to show that $\angle D'BD=0$.

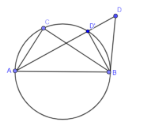
As you can see from this figure, when $\angle D'BD=0$ it means the line BD falls upon the line BD’ or the line BD has overlapped with BD’ and when the line BD and BD’ overlaps then point D and D’ will also coincide.