Question

If a line segment \[AM = \] \[a\] moves in the plane \[XOY\] remaining parallel to \[OX\] so that the left end point \[A\] slides along the circle \[{x^2} + {y^2} = {a^2}\] , the locus of \[M\] is
A) \[{x^2} + {y^2} = 4{a^2}\]
B) \[{x^2} + {y^2} = 2ax\]
C) \[{x^2} + {y^2} = 2ay\]
D) \[{x^2} + {y^2} - 2ax - 2ay = 0\]

Answer 1

Hint:
Here, we have to find the locus of M. The set of all points which form geometrical shapes such as a line, a line segment, circle, a curve, etc., and whose location satisfies the conditions is the locus.

Formula Used:
We will use the following formulas:
1) Equation of the circle is of the form \[{x^2} + {y^2} = {a^2}\] where \[x\] is the distance from the origin along the \[x\] axis, \[y\] is the distance from the origin along the \[y\] axis and \[a\] is the radius of the circle.
2) The square of the difference of two numbers is given by the algebraic identity \[{(a - b)^2} = {a^2} + {b^2} - 2ab\] where \[a\] and \[b\] are two numbers.

Complete step by step solution:
We are given a line segment in the plane \[XOY\] which is parallel to \[OX\]. The line segment \[AM = \] \[a\]lies in the plane \[XOY\]. The point \[A\] slides along the circle \[{x^2} + {y^2} = {a^2}\]. Let the coordinates of \[A\] be \[(x,y)\] and \[M\] be \[(\alpha ,\beta )\] .

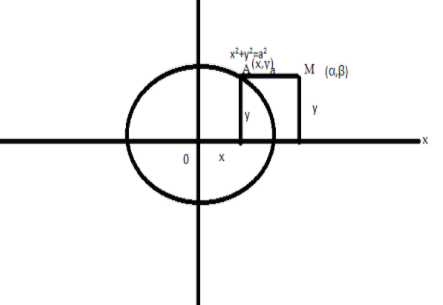
Since \[AM\] is parallel to \[OX\]
The points at \[M\] be \[OM = OX + XM\]
Here \[OM = \alpha \]; \[OX = x\] ; \[XM = a\] because \[\left[ {XM = AM} \right]\].
So, we have \[\alpha = x + a\] and \[\beta = y\]
Now, we have \[x = \alpha - a;y = \beta \]
So, the coordinates of \[M\] are \[(\alpha - a,\beta )\]
We know that the point \[A\] slides along the circle \[{x^2} + {y^2} = {a^2}\]
Since \[AM\] is a line segment, the point \[M\]also slides along the circle.
Substituting the coordinates of \[M\] in the equation of the circle, we have
\[ \Rightarrow {(\alpha - a)^2} + {\beta ^2} = {a^2}\]
The square of the difference of two numbers is given by the algebraic identity \[{(a - b)^2} = {a^2} + {b^2} - 2ab\] where \[a\] and \[b\] are two numbers.
Now, by using the algebraic identity, we get
\[ \Rightarrow ({\alpha ^2} + {a^2} - 2a\alpha ) + {\beta ^2} = {a^2}\]
Simplifying the equation, we have
\[ \Rightarrow {\alpha ^2} - 2a\alpha + {\beta ^2} = 0\]
Rewriting the equation, we have
\[ \Rightarrow {\alpha ^2} + {\beta ^2} = 2a\alpha \]
Since \[(\alpha ,\beta )\] are the coordinates of \[M\] , we have
\[ \Rightarrow {x^2} + {y^2} = 2ax\]

Therefore, the locus of \[M\] is \[{x^2} + {y^2} = 2ax\]

Note:
We know that a locus is a set of all the points whose position is defined by certain conditions. We have to find the location of \[M\]. We have important conditions to find out the locus. The locus at the fixed distance $d$ from the point $p$ is considered as a circle with $p$ as its center and $d$ as its diameter. Every point which satisfies the given geometrical condition lies on the focus. A point which does not satisfy the given geometrical condition cannot lie on the focus.