Question

If a line intercepted between the coordinate axes is trisected at a point \[A(4,3)\] which is nearer to x-axis, then its equation is
A. \[4x - 3y = 7\]
B. \[3x + 2y = 18\]
C. \[3x + 8y = 36\]
D. \[x + 3y = 13\]

Answer 1

Hint:Here we assume the x and y intercepts of the line and write the equation of line in intercept form. Then using the concept of trisection at point A we divide the line into two segments with the help of ratio. Using the section formula we write the coordinates of the point dividing the line into ratio and equate the coordinates to given coordinates to obtain the value of h and k.

Formula used:
a) General equation of a line having x intercept as h and y intercept as k is \[\dfrac{x}{h} + \dfrac{y}{k} = 1\]
b)Section formula states that if a point \[P(x,y)\] divides the line joining points \[A(a,b),B(c,d)\] in the ratio \[m:n\] internally then,
\[P(x,y) = \left( {\dfrac{{c.m + a.n}}{{m + n}},\dfrac{{d.m + b.n}}{{m + n}}} \right)\]

Complete step-by-step answer:
First we draw a diagram of a line having intercept h on x-axis and intercept k on y-axis. Intercept means the point where the line cuts that axis. Here x intercept is h so the point where the line meets the x-axis is \[(h,0)\] and y intercept is k so the point where the line meets the y-axis is \[(0,k)\].

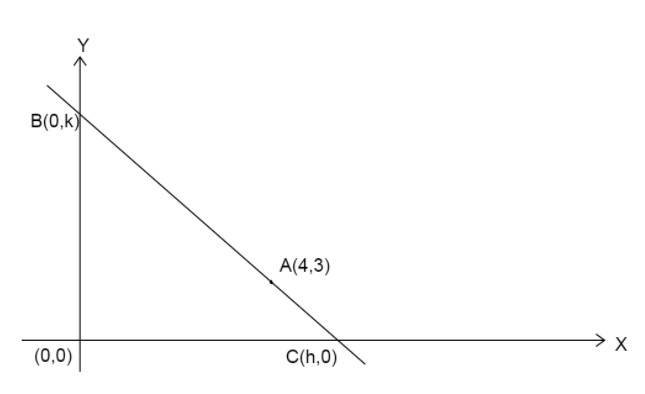
We have point \[C(h,0)\] which lies on the x-axis and \[B(0,k)\] which lies on the y-axis.
Let us assume equation of line be \[\dfrac{x}{h} + \dfrac{y}{k} = 1\] … (1)
We are given that the point \[A(4,3)\] is closer to the x-axis and the line is trisected means that the line is divided in the ratio \[1:2\] or \[2:1\]. Since, point \[A(4,3)\] is closer to the x-axis so the ratio of line segments \[BA:AC = 2:1\].
So, the point \[A(4,3)\] divides the line in ratio \[2:1\].
Now we know from section formula that the point which divides the line joining two points \[A(a,b),B(c,d)\] in the ratio \[m:n\] internally is given by \[P(x,y) = \left( {\dfrac{{c.m + a.n}}{{m + n}},\dfrac{{d.m + b.n}}{{m + n}}} \right)\]
Here points are \[B(0,k)\],\[C(h,0)\] and ratio is \[2:1\]
Substitute the value of \[a = 0,b = k,c = h,d = 0,m = 2,n = 1\]
\[
  A(4,3) = \left( {\dfrac{{h.2 + 0.1}}{{2 + 1}},\dfrac{{0.2 + k.1}}{{2 + 1}}} \right) \\
  A(4,3) = \left( {\dfrac{{2h}}{3},\dfrac{k}{3}} \right) \\
 \]
Now we equate the coordinates of the point to coordinate of \[A(4,3)\]
\[ \Rightarrow \dfrac{{2h}}{3} = 4\]
Cross multiply the denominator of LHS to RHS of the equation
\[
   \Rightarrow 2h = 4 \times 3 \\
   \Rightarrow 2h = 12 \\
 \]
Divide both sided by 2
\[
   \Rightarrow \dfrac{{2h}}{2} = \dfrac{{12}}{2} \\
   \Rightarrow h = 6 \\
 \]
Now,
\[ \Rightarrow \dfrac{k}{3} = 3\]
Cross multiply the denominator of LHS to RHS of the equation
\[
   \Rightarrow k = 3 \times 3 \\
   \Rightarrow k = 9 \\ \Rightarrow 3x + 2y = 18
 \]
So, the value of \[h = 6,k = 9\]
Substitute in equation (1) to obtain equation of the line
\[ \Rightarrow \dfrac{x}{6} + \dfrac{y}{9} = 1\]
Take LCM
\[ \Rightarrow \dfrac{{3x + 2y}}{{18}} = 1\]
Cross multiply the denominator of LHS to RHS of the equation
We get, $3x+2y = 18$

So, the correct answer is “Option B”.

Note:Students are likely to make mistake in substituting the values for a,b,c,d in the section formula as we choose the points according to the ratio, here ratio is \[2:1\],so we take the first point nearer to upper part in the ratio i.e. y intercept here and then second point nearer to the lower part in the ratio. Students get confused and write points in wrong places.