Question

If $ A = \left( { - 3,4} \right) $, $ B = \left( { - 1, - 2} \right) $, $ C = \left( {5,6} \right) $ and $ D = \left( {x, - 4} \right) $ are the vertices of a quadrilateral such that $ \Delta ABD = 2\Delta ACD $ . Then x, is equal to
A. $ 6 $
B. $ 9 $
C. $ 69 $
D. $ 96 $

Answer 1

Hint: In this question, we are given a quadrilateral ABCD with given dimensions and in which one dimension is unknown and we have to find that unknown variable. In the question, we had a condition $ \Delta ABD = 2\Delta ACD $ so, in this question we need to use the formula for triangle as
 $ ar(\Delta ) = \dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right| $

Complete step by step solution:
In the above question, we have to find the value of x, while we are provided with a quadrilateral with coordinates A, B, C, D with dimensions which is given in the question as
 $ A = \left( { - 3,4} \right) $
 $ B = \left( { - 1, - 2} \right) $
 $ C = \left( {5,6} \right) $
 $ D = \left( {x, - 4} \right) $
Firstly, drawing a quadrilateral and constructing a diagonal AD.

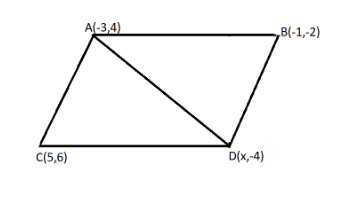
Now, using the formula
 $ ar(\Delta ) = \dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right| $
In $ \Delta ABD $ ,
 $ ar\left( {\Delta ABD} \right) = \dfrac{1}{2}\left| {\left( { - 3} \right)\left( { - 2 + 4} \right) + - 1\left( { - 4 - 4} \right) + x\left( {4 - ( - 2)} \right)} \right| $
 $
 = \dfrac{1}{2}\left| {2 + 6x} \right| \\
 = \left| {1 + 3x} \right| \ldots \ldots \left( 1 \right) \;
 $
Now, in $ \Delta ACD $
 $
 ar\left( {\Delta ACD} \right) = \dfrac{1}{2}\left| {\left( { - 3} \right)\left( {6 + 4} \right) + 5\left( { - 4 - 4} \right) + x\left( {4 - 6} \right)} \right| \\
 = \dfrac{1}{2}\left| { - 70 - 2x} \right| \\
 = 35 + x \ldots \ldots \left( 2 \right) \\
 \left( {\therefore \left| { - 1} \right| = 1} \right) \;
 $
We are given a condition in the question as $ \Delta ABD = 2\Delta ACD $ now substituting the values from the above two marked equations,
 $
 1 + 3x = 2(35 + x) \\
 1 + 3x = 70 + 2x \\
 69 = x \;
 $
 $ \Rightarrow x = 69 $
Hence, the value for x is $ 69. $
So, the correct answer is “Option C”.

Note: See the signs carefully while drawing the quadrilateral and make sure to draw the correct diagonal. We know that if the area of the triangle is zero then the three points are collinear, that is we will have a straight line. We also know that the sum of interior angles in a quadrilateral is 360 degrees but the sum of interior angles in a triangle is 180 degree.