Question

If a function is given as $ f'(x)=|x|-\{x\} $ where $ \{x\} $ is the fractional part of x, then f(x) is increasing in:
(a) $ \left( 0,1 \right) $
(b) $ \left( \dfrac{-1}{2},0 \right) $
(c) $ \left( \dfrac{1}{2},2 \right) $
(d) $ \left( \dfrac{1}{2},\infty \right) $

Answer 1

Hint: We know that the condition for an increasing function in an interval is $ f'(x)>0 $ at every point in that interval. We find an interval for x in which condition $ f'(x)>0 $ is satisfied. In order to find the interval we use the fact that \[\left\{ x \right\}=x-\left[ x \right]\] for all x, where $ \left[ . \right] $ is Greatest Integer Function and properties of $ \left| x \right|=x $ for $ x>0 $ , $ \left| x \right|=-x $ for $ x<0 $ .

Complete step-by-step answer:
Given that $ f'(x)=|x|-\{x\} $ , where $ \{x\} $ is the fractional part of x.
We need to find the interval in which f(x) is increasing.
We know that for a f(x) to become an increasing function in a given interval the following condition needs to be satisfied.
 $ f'(x)>0 $
According to the problem $ f'(x)=|x|-\{x\} $ . So,
 $ |x|-\{x\}>0 $
We know that fractional part of x ({x}) is defined as follows
Fractional part\[\{x\}=x-[x]\], where [.] is Greatest Integer function.
 $ \left| x \right|-\left( x-\left[ x \right] \right)>0.......(1) $
Since properties of modulus of x (|x|) changes with respect to value of x. We divide into two conditions for ‘x’ as follows:
 $ 1)x<0 $
 $ 2)x>0 $
Let us first find the interval for f(x) using condition (1).
We know for $ x<0 $ , $ |x|=-x $ .
Let us use this in equation (1).
 $ -x-(x-[x])>0 $
 $ -2x+[x]>0 $
 $ [x]>2x $
Since $ x<0 $ and $ \left[ x \right] $ takes the value of the greatest integer less than or equal to the value of x it varies from -1 to $ -\infty $ . So, we get $ 2x<-1 $ .
 $ x<\dfrac{-1}{2} $ .
We got $ f'(x)>0 $ in the interval $ \left( -\infty ,\dfrac{-1}{2} \right) $ .
Now we find the interval for f(x) using condition (2).
We know that for $ x>0 $ ,|x|=x.
Let us use this in equation (1).
 $ x-(x-[x]) $ >0
 $ x-x+[x]>0 $
 $ [x]>0 $
Since $ x>0 $ and $ [x] $ takes the value of the greatest integer less than or equal to the value of x, it varies from 0 to $ +\infty $ .
We also know that $ [x]=0 $ in the interval $ [0,1) $ .
So, we understood that x>1.
The interval in which $ f'(x)>0 $ is $ [1,\infty ) $ .
∴ The interval in which $ f'(x)>0 $ is $ \left( -\infty ,\dfrac{-1}{2} \right)\bigcap \left[ 1,\infty \right) $
We don’t have a correct option.

Note: Alternatively we can draw the plots of $ \left| x \right| $ and $ \left\{ x \right\} $ to check $ f'(x)>0 $ . Now we solve by using the idea for an alternative solution.
We know that for a f(x) to become an increasing function in a given interval the following condition needs to be satisfied.
 $ f'(x)>0......(1) $
We have $ f'(x)=|x|-\{x\} $ as given in the problem.
Using equation (1), we get $ \left| x \right|-\left\{ x \right\}>0 $
 $ \left| x \right|>\left\{ x \right\}......(2) $
Now from the plot we need to find the interval where condition in equation (2) holds true.
Let us plot curves $ y=\left| x \right| $ and $ y=\left\{ x \right\} $ .

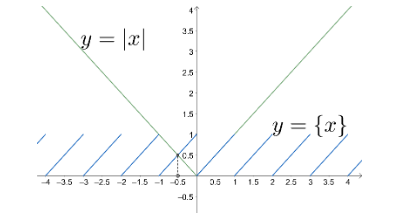
From above graph, we can observe that the value of $ \left| x \right| $ is greater than $ \left\{ x \right\} $ in interval $ \left( -\infty ,\dfrac{-1}{2} \right)\bigcap \left[ 1,\infty \right) $ .
You may confuse here as both plots coincide with each other in interval $ \left( 0,1 \right) $ . This makes $ f'(x)=0 $ which eventually makes f(x) constant in that interval.