Question

If a dipole of a dipole moment $\vec p$ is placed in a uniform electric field $\vec E$ , then torque acting on it is given by:
A) $\vec \tau = \vec p.\vec E$
B) $\vec \tau = \vec p \times \vec E$
C) $\vec \tau = \vec p + \vec E$
D) $\vec \tau = \vec p - \vec E$

Answer 1

Hint:Dipole moment is a product of charge and the dipole length. When a dipole is placed in a uniform electric field it experiences a torque which aligns to the direction of the electric field with zero net force. The torque acting on the dipole is given as the cross product of dipole moment and the electric field.

Complete step by step solution:
 Torque is the measure of the force that causes an object to rotate about an axis. We know that torque is a vector quantity, it has magnitude as well as direction.

The magnitude of torque $\vec \tau $ is calculated as follows:
$\tau = Fr\sin \theta $
Here $F$ is the force acting on the dipole,
$r$ is the length of the moment arm,
$\theta $ is the angle between the force vector and the moment arm.
But we need to find the torque in terms of dipole moment $\vec p$ .
Consider the following figure:

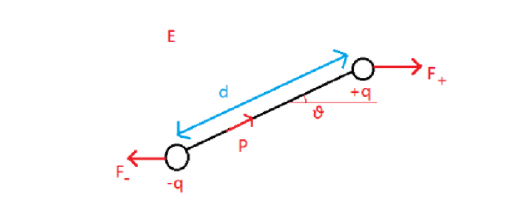
Diagram: self-drawn
The dipole moment of charges $q, - q$ separated by a distance $\vec d$ is given as
$\vec p = q\vec d$
Now, the force acting on the charges are as follows:
${\vec F_ + } = + q\vec E$
Here, ${\vec F_ + }$ denotes force acting on positive charge
$ + q$ denotes positive charge and
$\vec E$ is the uniform magnetic field.
Similarly, force acting on the negative charge ${\vec F_ - }$ will be
${\vec F_ - } = - q\vec E$

The components of force perpendicular to the dipoles is:

${\vec F_ + } = + q\vec E\sin \theta $
${\vec F_ - } = - q\vec E\sin \theta $
Now, torque is given as a perpendicular component of force acting on the dipole multiplied by the distance separating the force.
$ \Rightarrow \tau = F \times d$
But the magnitude of force is $q\vec E\sin \theta $ ,
$ \Rightarrow \vec \tau = q\vec E\sin \theta \times \vec d$
$ \Rightarrow \vec \tau = q\vec d\vec E\sin \theta $
But we know that $\vec p = q\vec d$ , substituting in above equation, we get
$ \Rightarrow \vec \tau = \vec p\vec E\sin \theta $
OR $\vec \tau = \vec p \times \vec E$

Thus, option B is the correct option.

Note:Torque, dipole moment, force and distance between the dipoles are vector quantities. They have magnitude as well as direction. Torque is the cross product of dipole moments with the force acting on the dipole. A dipole consists of two charges having equal magnitude but opposite charge.

.Subject:PHYSICS