Question

If a couple has three daughters, what are the chances that the fourth child will be a son?
A. $100\% $
B. \[75\% \]
C. \[50\% \]
D. \[0\% \]

Answer 1

Hint: The gender of an individual is decided by the genes the offspring inherits from the parents. The father can donate either a Y chromosome or an X chromosome. The mother can only donate an X chromosome. If the offspring receives two X chromosomes, they're going to be female. If the offspring inherits an X and a Y chromosome, they're going to be male.

Complete answer: There are two sex chromosomes X and Y. Humans are diploid having two sex chromosomes, in females a pair of the X chromosome is found while in males an X and Y chromosome is present. There is \[50\% \] chance that the subsequent child is going to be a boy because it entirely depends upon the chromosome of the sperm which fertilizes the ovum. Each pregnancy features a \[50\% \] chance of leading to a boy or girl and this doesn't include the likelihood of multiples. Having 3 daughters previously doesn't affect the probabilities of any resulting pregnancy. The prospect of getting a boy remains at \[50\% \].

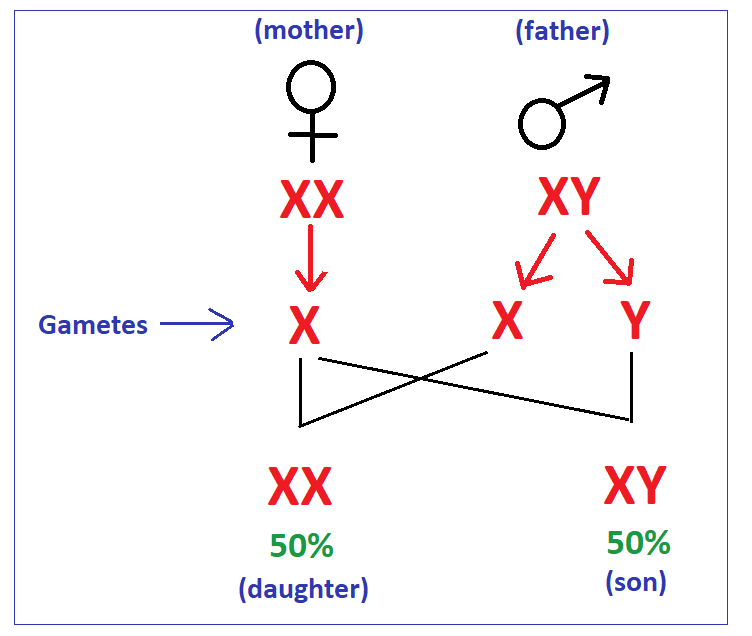
So, the correct answer is option C, i.e., \[50\% \]

Note: It is important to note that when the calculations are done with precision then, it is found that for the first child born the probability is $51.6\% $ of a boy, but after one girl it drops to $51.3\% $ or the second child, after two girls it drops to, $51\% $ then 50.6% and eventually furthermore after four girls.