Question

If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volume of the two parts.

Answer 1

Hint:Divide the cone into 2 equal halves. Find the radius and height of the smaller cone and the frustum formed. The ratio of volume will be the volume of the smaller cone to the frustum of the cone.

Complete step-by-step answer:
We have been given a cone with radius, R = 10 cm.

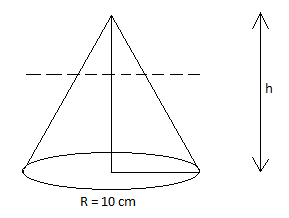
Let us consider the height of the cone as h cm. Now it is said that the cone is divided into 2 equal parts by drawing a plane through the mid-point of the axis, which is parallel to the base.
Here the upper part of the cone remains in the same shape but the bottom part will be a frustum.
We know that the volume of cone \[=V=\dfrac{1}{3}\pi {{r}^{2}}h\].
Now we need to find the volume of the frustum of the cone.
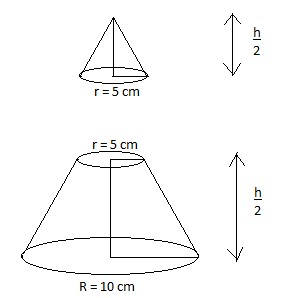
Here the height of cone = h cm, thus on dividing we get the frustum of the cone with radius, R = 10 cm and radius, r = 5 cm.
The height of frustum will be half of the total height \[=\dfrac{h}{2}\].
Similarly radius of the smaller cone, r = 5 cm and height of the smaller cone \[=\dfrac{h}{2}\] cm.
Thus volume of smaller cone, \[V=\dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{1}{3}\pi {{\left( 5 \right)}^{2}}\times \dfrac{h}{2}\].
Volume of frustum is given as,
 \[\begin{align}
  & V=\dfrac{1}{3}\pi \left[ {{R}^{2}}h-{{r}^{2}}h' \right]=\dfrac{1}{3}\pi \left( \dfrac{h}{2} \right)\left[ {{R}^{2}}+{{r}^{2}}+\operatorname{Rr} \right] \\
 & =\dfrac{1}{3}\pi \left( \dfrac{h}{2} \right)\left[ {{10}^{2}}+{{5}^{2}}+\left( 10\times 5 \right) \right] \\
 & =\dfrac{1}{3}\pi \left( \dfrac{h}{2} \right)\left[ 100+25+50 \right] \\
 & =\dfrac{1}{3}\pi \left( \dfrac{h}{2} \right)\left[ 175 \right] \\
\end{align}\]
\[\therefore \]Ratio of the volume \[=\dfrac{Volume\text{ }of\text{ }the\text{ }smaller\text{ }cone}{Volume\text{ }of\text{ }the\text{ }frustum\text{ }of\text{ }cone}\] \[=\dfrac{{}^{1}/{}_{3}\pi {{\left( 5 \right)}^{2}}\times {}^{h}/{}_{2}}{{}^{1}/{}_{3}\pi \left( {}^{h}/{}_{2} \right)\times 175}\]
Cancel out the similar terms from numerator and denominator.
\[\therefore \]Ratio of the volume \[=\dfrac{125}{175}=\dfrac{1}{7}\].
\[\therefore \]Volume of the smaller cone : volume of the frustum = 1 : 7
Thus we got the required ratio.
Note: The frustum is considered to be the difference of two right circular cones. Here we took the difference of the larger cone to the smaller cone. There are many examples of frustums that we use in ordinary day life like pot, glass, utensils etc.