Question

If a complex no: z satisfies $\left| 2z+10+10i \right|\le 5\sqrt{3}-5$, then the least principal argument of z is
$\begin{align}
  & \text{(a) }\dfrac{-5\pi }{6} \\
 & \text{(b) }\dfrac{-11\pi }{12} \\
 & \text{(c) }\dfrac{-3\pi }{4} \\
 & \text{(d) }\dfrac{-2\pi }{3} \\
\end{align}$

Answer 1

Hint:Given an expression is the equation of a circle in complex form. Find the center and radius and draw figure. Line y = x pass through the center of the circle, which we will get as in the third quadrant. Draw AO and BO as the tangent to the circle and find the argument i.e., angle where the tangent touches the circle.

Complete step-by-step answer:
We have been given a complex no: z and given the expression,
$\left| 2z+10+10i \right|\le 5\sqrt{3}-5$
Let us take 2 common from the expression
$\begin{align}
  & \left| 2z+5+5i \right|\le 5\sqrt{3}-5 \\
 & \left| z+5+5i \right|\le \dfrac{5\sqrt{3}-5}{2} \\
\end{align}$
Now as $\left( \dfrac{5\sqrt{3}-5}{2} \right)$ is less that $\left| z+5+5i \right|$ , the given equation of z is of a circle. Thus, let us find the center of the circle and radius from the expression,
$\left| z+5i+5 \right|\le \dfrac{5\sqrt{3}-5}{2}$
The general equation of a circle whose center is at point having affix ${{z}_{0}}$ and radius r is $\left| z-{{z}_{0}} \right|=r$.
Here, $\left| z-{{z}_{0}} \right|$$<$r, represents interior of a circle \[\left| z-{{z}_{0}} \right|=r\].
Here \[{{z}_{0}}=-\left( 5i+5 \right)\]
Hence our circle is (-5, -5) and radius, $r=\dfrac{5\sqrt{3}-5}{2}$
Now let us draw the figure with a circle, which has centre (-5, -5) and $r=\dfrac{5\sqrt{3}-5}{2}$. The y = x line passes through the centre of the circle. The circle is in the 3rd quadrant as the centre is (-5, -5).
We can rewrite y = x, into the general form of a slope-intercept equation y = mx + b.
Where m is the slope, whose value is 1 and b is zero. By putting m=1 and b=0 in the equation, we get y = x.
Now z represents the boundary of the circle and the interior of the circle. Thus, the minimum can be found by drawing a tangent line to the circle.

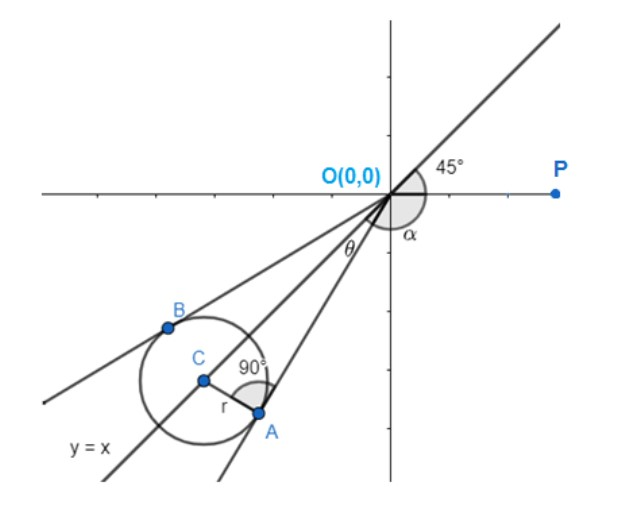
Now point A represents minimum argument and point B represents maximum argument.
i.e.,
$\begin{align}
  & {{\text{z}}_{\text{A}}}\text{ = minimum argument} \\
 & {{\text{z}}_{\text{B}}}\text{ = max argument} \\
\end{align}$
We are asked to find the least principal argument of z, which means that we need to find ${{z}_{A}}$. Thus, we need to find the angles POA (from the figure). If we join AC, it will be the radius of the circle as well as the perpendicular because that is the point of tangency. The tangent to a circle is always perpendicular to the radius.
Let us take $\angle COA=\theta $ (from figure)
Thus $\text{sin }\!\!\theta\!\!\text{ = }\dfrac{\text{opposite side}}{\text{hypotenuse}}$ by considering $\Delta COA$, right-angled at A.
$\sin \theta =\dfrac{AC}{OC}=\dfrac{r}{OC}$ ……………. (i)
By using distance formulas, we can find the value of OC.
Distance formula$=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
 $\begin{align}
  & O\left( 0,0 \right)=\left( {{x}_{1}},{{y}_{1}} \right),C\left( -5,-5 \right)=\left( {{x}_{2}},{{y}_{2}} \right) \\
 & \therefore \text{distance OC} \\
 & =\sqrt{{{\left( -5-0 \right)}^{2}}+{{\left( -5-0 \right)}^{2}}}=\sqrt{{{5}^{2}}+{{5}^{2}}} \\
 & =\sqrt{25+25}=\sqrt{50}=5\sqrt{2} \\
\end{align}$
Hence, we got $OC=5\sqrt{2}$ and we know $r=\left( \dfrac{5\sqrt{3}-5}{2} \right)$ , now put there in equation (i), we get
$\begin{align}
  & \sin \theta =\dfrac{\left( \dfrac{5\sqrt{3}-5}{2} \right)}{5\sqrt{2}}=\dfrac{5\left( \sqrt{3}-1 \right)}{5\times 2\sqrt{2}}=\dfrac{\sqrt{3}-1}{2\sqrt{2}} \\
 & \therefore \sin \theta =\dfrac{\sqrt{3}-1}{2\sqrt{2}}=\sin 15 \\
\end{align}$
$\theta ={{15}^{\circ }}$
Now from the figure the y = x line bisects the axis, and the line y =x makes an angle of ${{45}^{\circ }}$with the x-axis.
Take angle POA as $\alpha $ .
Hence
$\begin{align}
  & {{45}^{\circ }}+\alpha +\theta ={{180}^{\circ }} \\
 & \therefore {{45}^{\circ }}+\alpha +{{15}^{\circ }}={{180}^{\circ }} \\
 & \alpha =180-45-15 \\
 & =180-60={{120}^{\circ }} \\
\end{align}$
Thus, we got the angle as ${{120}^{\circ }}=\dfrac{2\pi }{3}$
Thus, the minimum argument (z) becomes $\left( -\dfrac{2\pi }{3} \right)$, as the $\alpha $ is taken in clockwise motion, the argument is negative.
Thus, we got the least principal argument of z as $\left( \dfrac{-2\pi }{3} \right)$.
$\therefore $ option (d) is correct.

Note: The general equation of the circle is actually $z\overline{z}+a\overline{z}+\overline{a}z+b=0$ where a is a complex number and $b\in R$. The center and radius are (-a), $\sqrt{{{\left| a \right|}^{2}}-b}$ respectively. Here we were asked to find the least principal argument of z, hence we found ${{z}_{A}}$ . But if it was the maximum argument then take POB.