Question

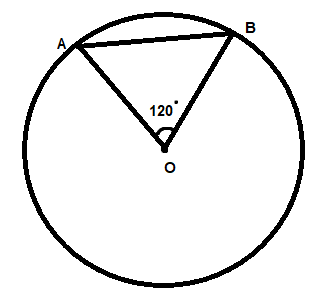
If a chord 8 inches long has an arc of ${120^ \circ }$, the radius in inches of the circle is
A. 4
B. $4\sqrt 3 $
C. $\dfrac{{8\sqrt 3 }}{5}$
D. $\dfrac{{8\sqrt 3 }}{3}$
E. $2\sqrt 3 $

Answer 1

Hint: First let's do the required construction, and we know that OB is the radius and we need to draw a line OC perpendicular to AB and extend it to a point D on the arc AB bisecting the angle formed by the chord and we get $\angle BOC = {60^ \circ }$ and $\angle BCO = {90^ \circ }$ and using angle sum property we can find angle B and using sine ratio we find the value of OC and applying Pythagoras theorem in triangle ABC we get the required radius.

Step by step solution :
Now we have a circle with centre O
We have a chord AB
We know that OB is the radius of the circle

Now let's draw a line OC perpendicular to AB and extend it to a point D on the arc AB
The line bisects the angle formed by the chord

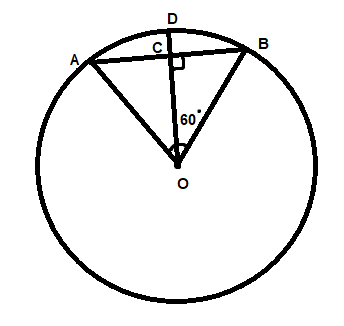
Hence we have $\angle BOC = {60^ \circ }$ and $\angle BCO = {90^ \circ }$
Therefore in the triangle OBC , using angle sum property we get
$
   \Rightarrow \angle BOC + \angle BCO + \angle CBO = {180^ \circ } \\
   \Rightarrow {60^ \circ } + {90^ \circ } + \angle CBO = {180^ \circ } \\
   \Rightarrow {150^ \circ } + \angle CBO = {180^ \circ } \\
   \Rightarrow \angle CBO = {180^ \circ } - {150^ \circ } = {30^ \circ } \\
 $
Hence by using this we can find OC
$
   \Rightarrow \sin 30 = \dfrac{{OC}}{{OB}} \\
   \Rightarrow \dfrac{1}{2} = \dfrac{{OC}}{r} \\
   \Rightarrow \dfrac{r}{2} = OC \\
 $
Now considering the triangle OBC we have BC = 4 inches and OB=r and OC = $\dfrac{r}{2}$
Using Pythagoras theorem we get
$
   \Rightarrow {r^2} = {4^2} + {\left( {\dfrac{r}{2}} \right)^2} \\
   \Rightarrow {r^2} = 16 + {\dfrac{r}{4}^2} \\
   \Rightarrow {r^2} - {\dfrac{r}{4}^2} = 16 \\
   \Rightarrow {\dfrac{{4{r^2} - r}}{4}^2} = 16 \\
   \Rightarrow 3{r^2} = 64 \\
   \Rightarrow {r^2} = \dfrac{{64}}{3} \\
   \Rightarrow r = \sqrt {\dfrac{{64}}{3}} = \dfrac{8}{{\sqrt 3 }} \\
 $
Hence now multiplying and dividing by $\sqrt 3 $ we get
 $ \Rightarrow r = \dfrac{8}{{\sqrt 3 }}\times \dfrac{{\sqrt 3 }}{{\sqrt 3 }} = \dfrac{{8\sqrt 3 }}{3}$
Hence we get the radius

Therefore the correct answer is option C.

Note :
A chord of a circle is a straight line segment whose endpoints both lie on the circle. The infinite line extension of a chord is a secant line, or just secant.
In a circle, if two chords are equidistant from the center of a circle, then the two chords are equal in measure.