Question

If A, B, C, D are angles of a cyclic quadrilateral, then prove that cos A + cos B + cos C + cos D = 0.

Answer 1

Hint: First of try to recollect what cyclic quadrilateral is. Now, we know that in a cyclic quadrilateral, opposite angles are supplementary, so replace C by (180 – A) and D by (180 – B) and use \[\cos \left( 180-\theta \right)=-\cos \theta \] to prove the desired result.

Complete step-by-step answer:

In this question, we are given that A, B, C, D are angles of a cyclic quadrilateral. We have to prove that cos A + cos B + cos C + cos D = 0. Before proceeding with this question, let us see what cyclic quadrilateral is. A cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose all vertices lie on a single circle. This circle is called circumcircle and vertices are said to be cyclic. In a cyclic quadrilateral, the sum of the opposite angles is always \[{{180}^{o}}\] , or in other words, we can say that the opposite angles of the cyclic quadrilateral are supplementary.

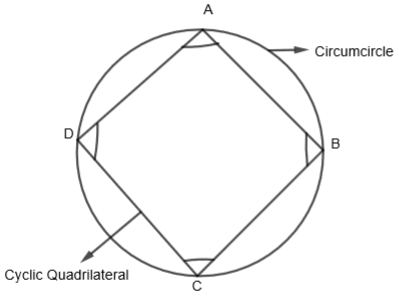
The above figure is of a cyclic quadrilateral. In the above figure,

\[\angle A+\angle C={{180}^{o}}\]

\[\angle B+\angle D={{180}^{o}}\]

Now, let us consider our question. Let us take the LHS of the equation given in the question, we get,

\[LHS=\cos A+\cos B+\cos C+\cos D.....\left( i \right)\]

We know that in a cyclic quadrilateral,

\[A+C={{180}^{o}}\]

\[\Rightarrow C={{180}^{o}}-A\]

By substituting the value of C in equation (i), we get,

\[LHS=\cos A+\cos B+\cos \left( {{180}^{o}}-A \right)+\cos D.....\left( ii \right)\]

Again, we know that in a cyclic quadrilateral,

\[B+D={{180}^{o}}\]

\[\Rightarrow D={{180}^{o}}-B\]

By substituting the value of D in equation (ii), we get,

\[LHS=\cos A+\cos B+\cos \left( {{180}^{o}}-A \right)+\cos \left( {{180}^{o}}-B \right)\]

We know that, \[\cos \left( {{180}^{o}}-\theta \right)=-\cos \theta \]. By using this in the above equation, we get,

\[LHS=\cos A+\cos B-\cos A-\cos B\]

By canceling the like terms of the above equation, we get,

\[LHS=0+0=0\]

So, we get, LHS = RHS

Hence proved.

Here, we have proved that in a cyclic quadrilateral, cos A + cos B + cos C + cos D = 0 where A, B, C, and D are angles of a quadrilateral.

Note: First of all, students must remember the properties of the cyclic quadrilateral and should always try to name the vertices in order because then only we will get \[A+C={{180}^{o}}\] and \[B+D={{180}^{o}}\]. Some students make the mistake of naming the vertices differently and still use the same formulas which is wrong. In that case, students should only remember that the sum of the opposite angles of a cyclic quadrilateral is \[{{180}^{o}}\].