Question

If a, b are the segments of a focal chord and 2c is the latus rectum of a parabola, then prove that \[{{a}^{3}}+{{b}^{3}}\ge 2{{c}^{3}}\]

Answer 1

Hint: For solving this problem we use the formula of semi latus rectum that is if a, b are the segments of focal chord and 2c is the latus rectum of any parabola then \[c=\dfrac{2ab}{a+b}\]. This is applicable to any parabola. For any parabola, the latus rectum and segments of the focal chord are shown below

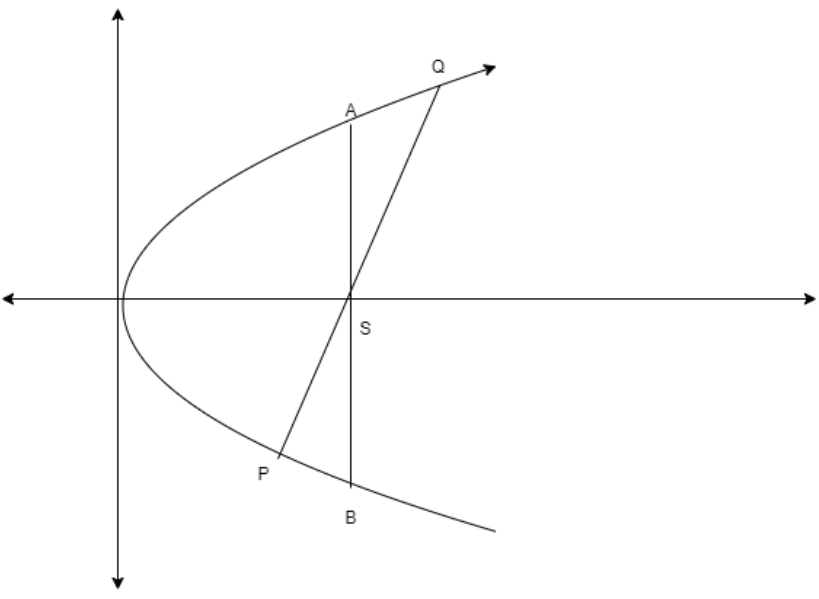
Here,\['S'\] is focus, \['AB=2c'\] is the latus rectum because it is perpendicular to axis and \['PS=a,SQ=b'\] are the segments of the focal chord of parabola. The latus rectum is also a focal chord but it is a special case, which is perpendicular to the axis of the parabola. Then we use the condition \[A.M\ge G.M\ge H.M\], where A.M is arithmetic mean, G.M is a geometric mean, and H.M is harmonic mean. We use these two conditions and get the required result.

Complete step-by-step solution
We are given that a, b are segments of focal chord and 2c is the semi latus rectum then the semi latus rectum is given as
\[c=\dfrac{2ab}{a+b}\].
We know that the arithmetic mean of a, b is given as
\[A.M=\dfrac{a+b}{2}\]
Now, we know that the geometric mean of a, b can be written is given as
\[G.M=\sqrt{ab}\]
We know that the harmonic mean of a, b can be written is given as
\[H.M=\dfrac{2ab}{a+b}\]
We know the standard condition that is
\[A.M\ge G.M\ge H.M\]
By substituting A.M, G.M, and H.M in \[A.M\ge G.M\ge H.M\] we will get
\[\dfrac{a+b}{2}\ge \sqrt{ab}\ge \dfrac{2ab}{a+b}\]
Now let us take the first condition that is \[A.M\ge G.M\] and by solving we will get
\[\Rightarrow \dfrac{a+b}{2}\ge \sqrt{ab}\]
Since, a, b are lengths squaring on both sides will have no effect.
By squaring on both sides we will get
\[\Rightarrow {{\left( a+b \right)}^{2}}\ge 4ab\]
By multiplying \[\left( a+b \right)\] on both sides we get
\[\begin{align}
  & \Rightarrow {{\left( a+b \right)}^{3}}\ge 4ab\left( a+b \right) \\
 & \Rightarrow {{a}^{3}}+{{b}^{3}}+3ab\left( a+b \right)\ge 4ab\left( a+b \right) \\
 & \Rightarrow {{a}^{3}}+{{b}^{3}}\ge ab\left( a+b \right) \\
\end{align}\]
Now let us consider the other part that is \[A.M\ge H.M\] we get
\[\Rightarrow \dfrac{a+b}{2}\ge \dfrac{2ab}{a+b}\]
Now let us substitute \[c=\dfrac{2ab}{a+b}\] in the above equation.
By cubing on both sides we will get
\[\begin{align}
  & \Rightarrow {{\left( a+b \right)}^{3}}\ge 8{{c}^{3}} \\
 & \Rightarrow {{a}^{3}}+{{b}^{3}}+3ab\left( a+b \right)\ge 8{{c}^{3}} \\
&\Rightarrow 3ab\left( a+b \right)\ge 8{{c}^{3}}-\left( {{a}^{3}}+{{b}^{3}} \right)..........equation(i) \\
\end{align}\]
Now by taking the equation \[{{a}^{3}}+{{b}^{3}}\ge ab\left( a+b \right)\] and by multiplying by 3 we get
\[\begin{align}
  & \Rightarrow {{a}^{3}}+{{b}^{3}}\ge ab\left( a+b \right) \\
 & \Rightarrow 3{{a}^{3}}+3{{b}^{3}}\ge 3ab\left( a+b \right)..........equation(ii) \\
\end{align}\]
By combining the equation (i) and equation (ii) we get
\[\begin{align}
&\Rightarrow 3{{a}^{3}}+3{{b}^{3}}\ge 3ab\left( a+b \right)\ge 8{{c}^{3}}-\left( {{a}^{3}}+{{b}^{3}} \right) \\
 & \Rightarrow 3{{a}^{3}}+3{{b}^{3}}\ge 8{{c}^{3}}-\left( {{a}^{3}}+{{b}^{3}} \right) \\
 & \Rightarrow 4\left( {{a}^{3}}+{{b}^{3}} \right)\ge 8{{c}^{3}} \\
 & \Rightarrow \left( {{a}^{3}}+{{b}^{3}} \right)\ge 2{{c}^{3}} \\
\end{align}\]
Hence proved.

Note: The important part in this question is taking the sign of the equation that is taking \[\ge \] is important. Due to inequality, students have to take care of where we need to change the inequality. Here, since all the values of a, b, c are natural numbers there will be no need to change the inequality. But some students will change the inequality after squaring on both sides. That is the only point that needs to be taken care of.