Question

If $A$ and $B$ are two sets, then $\left( {A \cap B} \right)'$ is equal to
A. $A' \cap B'$
B. $A' \cup B'$
C. $A \cap B$
D. $A \cup B$

Answer 1

Hint: Here in this problem, an incomplete statement is given. We need to complete the given incomplete statement. We all know De Morgan's laws that are often used in set theory. One of the statements given by De Morgan is the given incomplete statement. Using the law, we can able to complete the given statement.

Complete step by step answer:
Using De Morgan’s law, we have$\left( {A \cap B} \right)' = A' \cup B'$
We shall prove this statement.
Let $P = \left( {A \cap B} \right)'$ and $Q = A' \cup B'$
Let $x \in P$
Then, $x \in \left( {A \cap B} \right)'$
$ \Rightarrow x \notin \left( {A \cap B} \right)$
$ \Rightarrow x \notin A$ or$x \notin B$
$ \Rightarrow x \in A'$ or$x \in B'$
$ \Rightarrow x \in A' \cup B'$
$ \Rightarrow x \in Q$
Hence, we get$P \subset Q$ …………$\left( 1 \right)$
Now, let$y \in Q$
$ \Rightarrow y \in A' \cup B'$
$ \Rightarrow y \in A'$ or$y \in B'$
$ \Rightarrow y \notin A$ or$y \notin B$
\[\;\; \Rightarrow y \notin \left( {A \cap B} \right)\]
$ \Rightarrow y \in \left( {A \cap B} \right)'$
$ \Rightarrow y \in P$
Hence, we get$Q \subset P$ …………$\left( 2 \right)$
Now, we shall combine the first and second equations.
Thus, we get$P = Q$
That is$\left( {A \cap B} \right)' = A' \cup B'$
Let us consider the left-hand side$\left( {A \cap B} \right)'$.
Let us analyze the following Venn diagram.

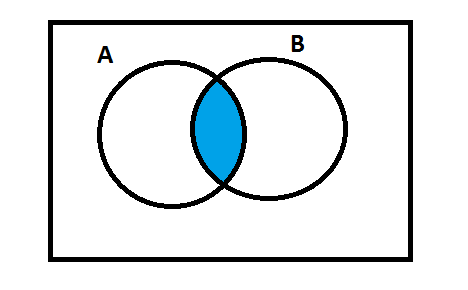
This diagram shows$A \cap B$. The blue-colored area is the intersection of$A$ and$B$.
Now, let us analyze the following diagram.

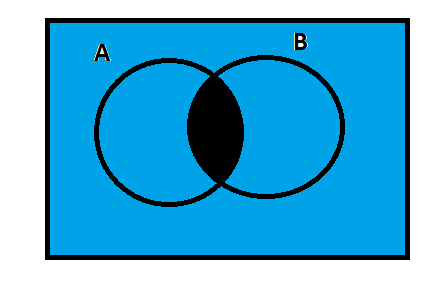
This diagram shows$\left( {A \cap B} \right)'$ and the blue-colored area is$\left( {A \cap B} \right)'$.
Hence we got the required left-hand side expression.
Now, we get into the right-hand side expression$A' \cup B'$.
Now, let us analyze the following diagram.

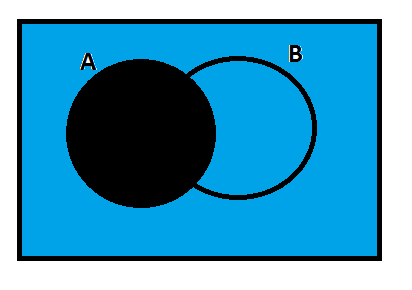
This diagram shows$A'$ and the black-colored area is required$A'$.
Now, let us analyze the following diagram.

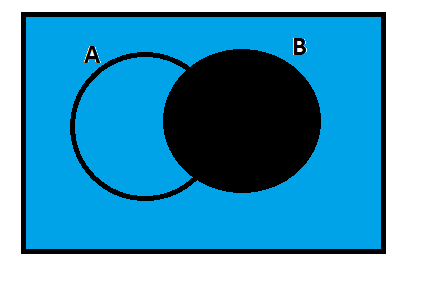
The above diagram shows\[B'\] and the black-colored area is required\[B'\].
Now, let us analyze the following diagram.

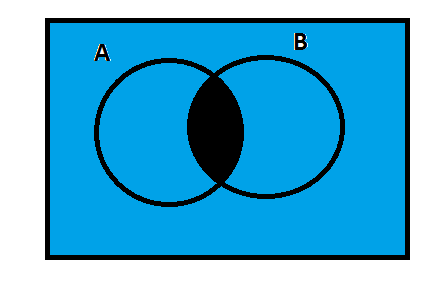
The above diagram shows$A' \cup B'$ and the blue-colored area is required\[B'\].
Hence we got the required left-hand side expression.
Therefore, we proved the statement $\left( {A \cap B} \right)' = A' \cup B'$using the Venn diagram.
So, the correct answer is “Option B”.

Note: Here we were asked to complete the famous theorem written by Demorgan. Since we know the de Morgan laws, we easily find the required answer. Also, we have proved this statement mathematically. The Venn-diagram representation will be easier to prove this statement. We all prefer pictorial representation. So, we have proved this statement using the Venn diagram too. Therefore, we proved the statement $\left( {A \cap B} \right)' = A' \cup B'$