Question

If $ A $ and $ B $ are two non-zero vectors having equal magnitude, the angle between the vectors $ A $ and $ A - B $ is:
(A) $ {0^0} $
(B) $ {90^0} $
(C) $ {180^0} $
(D) Dependent on the orientation of $ A $ and $ B $

Answer 1

Hint :Here, we have been given the two vectors and they both have equal magnitude and we have to find the angle between their subtractions. To find out this we have to use the parallelogram law of vector addition and then subtract these vectors.

Complete Step By Step Answer:
Let us first consider the vectors $ A $ and $ B $ as shown in the figure below and these vectors have magnitudes which are equal.

From the above figure we have $ \theta $ is the angle between the vectors $ A $ and $ B $
Now, by applying parallelogram law we can find out the angle between resultant vector between vectors $ A $ and $ B $ and vector $ A $ the angle is given by:
 $ \tan \phi = \dfrac{{B\sin \theta }}{{A + B\cos \theta }} $
Above equation gives the direction of the resultant vector, also we have the magnitudes of these vectors equal thus the above equation is written as:
 $ \Rightarrow \tan \phi = \dfrac{{\sin \theta }}{{1 + \cos \theta }} $ … (Since, $ A = B $ )
Now by using trigonometric identities we can write the above equation as:
 $ \sin \theta = \dfrac{{2\tan \dfrac{\theta }{2}}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}} $ and $ \cos \theta = \dfrac{{1 - {{\tan }^2}\dfrac{\theta }{2}}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}} $
Therefore,
 $ \Rightarrow \tan \phi = \dfrac{{\dfrac{{2\tan \dfrac{\theta }{2}}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}}}}{{1 + \dfrac{{1 - {{\tan }^2}\dfrac{\theta }{2}}}{{1 + {{\tan }^2}\dfrac{\theta }{2}}}}} $
On solving this equation, we get
 $ \Rightarrow \tan \phi = \dfrac{{2\tan \dfrac{\theta }{2}}}{{1 + {{\tan }^2}\dfrac{\theta }{2} + 1 - {{\tan }^2}\dfrac{\theta }{2}}} $
 $ \Rightarrow \tan \phi = \dfrac{{2\tan \dfrac{\theta }{2}}}{2} $
 $ \Rightarrow \tan \phi = \tan \dfrac{\theta }{2} $
 $ \Rightarrow \phi = \dfrac{\theta }{2} $
Thus, the angle between the resultant vector and the vector $ A $ is $ \phi = \dfrac{\theta }{2} $ .
Now, it has been asked that the angle between vector $ A $ and $ \vec A - \vec B $ by using the diagram given below:

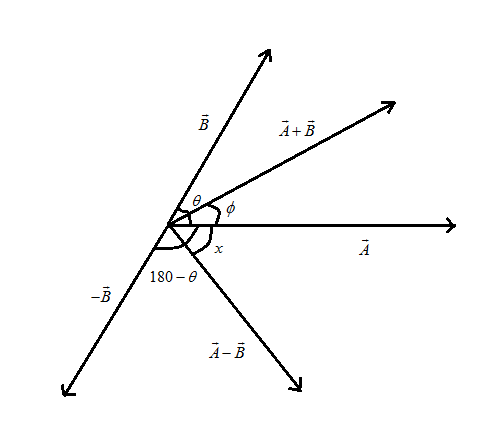
As we have obtained the angle between the $ \vec A + \vec B $ and $ \vec A $ that it is half of the angle $ \theta $ , so we can say that the angle between $ \vec A - \vec B $ and $ \vec A $ is given as:
 $ x = \dfrac{{180 - \theta }}{2} $ or $ x = 90 - \dfrac{\theta }{2} $
Hence, the angle between $ \vec A - \vec B $ and $ \vec A $ are dependent on orientation of $ \vec A $ and $ \vec B $ .
So, the correct answer is the option D.

Note :
Here, we have used the parallelogram law of vector addition. From this we can obtain the angle between the resultant of two vectors and one from the two vectors. So, we have discussed the angle and it is half of the angle between the two vectors. This shows that the direction of the resultant vector depends on the orientation of other two vectors.