Question

If A and B are two events such that $P(A) \ne 0$ and $P(B\left| {A) = 1} \right.$,then
A. $A \subset B$
B. $B \subset A$
C. $B = \phi $
D. $A = \phi $

Answer 1

Hint: For solving such questions we need understanding of the concept of set, subset and superset and formulae of probability chapters. Doing this will solve the question.

Complete step by step answer:
Given,
$P(A) \ne 0$ and $P(B\left| {A) = 1} \right.$
As $P(B\left| {A) = 1} \right.$ and we know that \[P(B\left| {A)} \right.\]=\[\dfrac{{P(B \cap A)}}{{P(A)}}\].
Therefore, $\dfrac{{P(B \cap A)}}{{P(A)}} = 1$
$P(B \cap A) = P(A)$
The conditional probability formula is derived from the probability multiplication law, P(A and B) = P(A)*P(B). You can also see this law as P(A). The Union sign (nominated) means "and" as in the case of A happening and the case B occurring.
This means that, probability of event occurring in$(B \cap A)$=probability of event occurring in A.
Which is only possible when $B \cap A$ is a subset of A

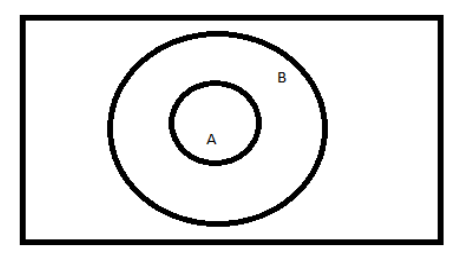
i.e.

Hence, the answer to this question is $A \subset B$.

Note: In such type of questions we need to understand each line of the question and understand the basic concepts of chapter as they help us in solving such type of questions and formulae like \[P(B\left| {A)} \right.\]=\[\dfrac{{P(B \cap A)}}{{P(A)}}\] which represents conditional probability.