Question

If A and B are any two events such that $P\left( A \right) = \dfrac{2}{5}$ and $P\left( {A \cap B} \right) = \dfrac{3}{{20}}$. Find the conditional probability,$P\left( {A|\left( {A' \cup B'} \right)} \right)$, where $A'$ denotes the complement of A.
(A) $\dfrac{5}{{17}}$
(B) $\dfrac{{11}}{{20}}$
(C) $\dfrac{1}{4}$
(D) $\dfrac{8}{{17}}$

Answer 1

Hint:Write down the formula for conditional probability, i.e.\[P\left( {A|B} \right) = \dfrac{{P\left( {A \cap B} \right)}}{{P(B)}}\]for the given problem first. Now work with the numerator and denominator parts separately. Use De Morgan’s Law for the denominator and Venn diagram for the numerator. Change them in the form of the given probabilities $P\left( A \right)$ and$P\left( {A \cap B} \right)$.

Complete step-by-step answer:
Let’s first try to analyse the information given in the question. Here the probability of the event A is given as $P\left( A \right) = \dfrac{2}{5}$ and the probability of event A and B is given as $P\left( {A \cap B} \right) = \dfrac{3}{{20}}$. And using that given information we need to find the conditional probability $P\left( {A|\left( {A' \cup B'} \right)} \right)$.

Before moving towards the solution we should understand the concept of conditional probability. The conditional probability of an event A is the probability that the event will occur given the knowledge that an event B has already occurred. This probability is written$P\left( {A|B} \right)$, a notation for the probability of A given B.
If events A and B are not independent, then the probability of the intersection of A and B (the probability that both events occur) is defined by:
\[P\left( {A \cap B} \right) = P\left( B \right) \times P\left( {A|B} \right) \Rightarrow P\left( {A|B} \right) = \dfrac{{P\left( {A \cap B} \right)}}{{P(B)}}\]
Therefore, by the same definition, the given expression will be:
$ \Rightarrow P\left( {A|\left( {A' \cup B'} \right)} \right) = \dfrac{{P\left( {A \cap \left( {A' \cup B'} \right)} \right)}}{{P\left( {A' \cup B'} \right)}}.................(1)$
Now, let’s simplify the probability $P\left( {A' \cup B'} \right)$using the concepts of set theory.
Using De Morgan’s Law, which states that the complement of the intersection of sets A and B is equal to the union of $A'$ and$B'$, i.e. ${\left( {A \cap B} \right)^\prime } = A' \cup B'$. And also the complement of the union of sets A and B is equal to the intersection of $A'$ and $B'$, i.e. ${\left( {A \cup B} \right)^\prime } = A' \cap B'$.

Therefore, by using De Morgan’s Law, we can simplify as: $P\left( {A' \cup B'} \right) = P\left( {{{\left( {A \cap B} \right)}^\prime }} \right)$
And since, the probability of the complement of an event is the probability of that event subtracted from universal $ \Rightarrow P\left( {A'} \right) = 1 - P\left( A \right)$
So, our probability $P\left( {A' \cup B'} \right)$ can be further solved as:
$ \Rightarrow P\left( {A' \cup B'} \right) = P\left( {{{\left( {A \cap B} \right)}^\prime }} \right) = 1 - P\left( {A \cap B} \right)$
But the probability of the intersection of A and B is already known, i.e. $P\left( {A \cap B} \right) = \dfrac{3}{{20}}$
$ \Rightarrow P\left( {A' \cup B'} \right) = 1 - P\left( {A \cap B} \right) = 1 - \dfrac{3}{{20}} = \dfrac{{20 - 3}}{{20}} = \dfrac{{17}}{{20}}..........................(2)$
So, we got the denominator value of (1), and now we have to figure out the value for the numerator, i.e. $P\left( {A \cap \left( {A' \cup B'} \right)} \right)$

For that, we can take the use of the Venn diagram, where we represent the two sets as circles and then shade the region that is to be studied. And these circles will be inside a rectangle, which is our universal set.

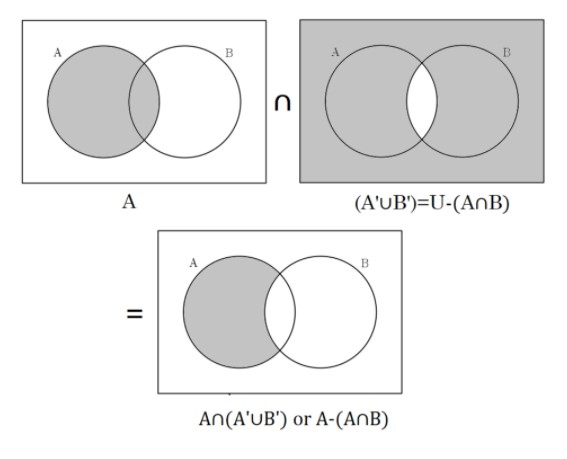
$ \Rightarrow $We can now conclude from the Venn diagram that: $P\left( {A \cap \left( {A' \cup B'} \right)} \right) = P\left( {A - \left( {A \cap B} \right)} \right) = P\left( A \right) - P\left( {A \cap B} \right)$
But we already have the probability values of $P\left( A \right) = \dfrac{2}{5}$ and $P\left( {A \cap B} \right) = \dfrac{3}{{20}}$, let’s substitute them
\[ \Rightarrow P\left( {A \cap \left( {A' \cup B'} \right)} \right) = P\left( A \right) - P\left( {A \cap B} \right) = \dfrac{2}{5} - \dfrac{3}{{20}} = \dfrac{{8 - 3}}{{20}} = \dfrac{5}{{20}} = \dfrac{1}{4}\]
Thus, we found the simplified forms of both numerator and denominator of relation (1), so we can rewrite it by using (2) and the above relation as:
$ \Rightarrow P\left( {A|\left( {A' \cup B'} \right)} \right) = \dfrac{{P\left( {A \cap \left( {A' \cup B'} \right)} \right)}}{{P\left( {A' \cup B'} \right)}} = \dfrac{{\dfrac{1}{4}}}{{\dfrac{{17}}{{20}}}} = \dfrac{{1 \times 20}}{{4 \times 17}} = \dfrac{5}{{17}}$
Therefore, we get the value for the required probability as $\dfrac{5}{{17}}$

So, the correct answer is “Option A”.

Note: In probability, always follow a step by step procedure for avoiding complications. The denotation $P\left( X \right)$ just means ‘probability of an event X’ and this X follows the rules of set theory. So you can use the methods of transformation with probabilities also. An alternative approach to this problem could be the use of rules of set theory like duality while solving instead of Venn diagrams. But solving with a Venn diagram will always help you visualize the problem better.