Question

If A (2, -3) and B (-2, 1) are two vertices of a triangle and third vertex moves on the line 2x + 3y = 9, then the locus of the centroid of the triangle is:
(a) 2x + 3y = 3
(b) 2x – 3y = 1
(c) x – y = 1
(d) 2x + 3y = 1

Answer 1

Hint: Find the coordinates of C from 2x + 3y = 9, find the y – coordinate. Hence find C (x, y). Use the centroid formula of triangles and get the centroid. The locus of centroid. The locus of centroid is equal to (h, k). Solve and get the equation for locus of the centroid of the triangle.

Complete step-by-step solution -
Let us consider the triangle as ABC. We have been given two vertices as A (2, -3) and B (-2, 1). Now it is said that the third vertex moves with the line, \[2x+3y=9\] ------ (1)
Let us consider the \[{{3}^{rd}}\] vertex as C. Let the x – coordinate be x.

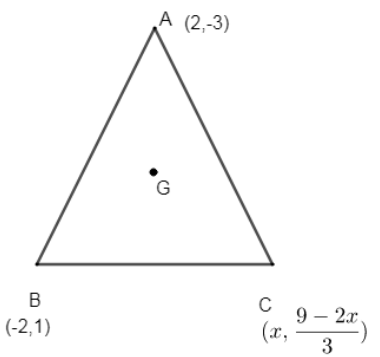
Thus from (1) let us find the y – coordinate,
\[2x+3y=9\]
\[\begin{align}
  & 3y=9-2x \\
 & \Rightarrow y=\dfrac{9-2x}{3} \\
\end{align}\]
Thus we can say that the coordinates of C = \[\left( x,\dfrac{9-2x}{3} \right)\].
The centroid is the center point of the triangle, marked as G. The point in which the three medians of the triangle intersect is known as the centroid of the triangle. The centroid of the triangle can be calculated by taking the average of X and Y coordinate points of all three vertices. Therefore the centroid of a triangle can be written as,
Centroid of a triangle = \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\] --- (2)
The locus of centroid is equal to (h, k).
Locus is a path on which a point can move, satisfying the conditions. The locus of centroid of a triangle is the point of concurrency of its three medians.
Let us put, \[\left( {{x}_{1}},{{y}_{1}} \right)=\left( 2,-3 \right)\]
\[\begin{align}
  & \left( {{x}_{2}},{{y}_{2}} \right)=\left( -2,1 \right) \\
 & \left( {{x}_{3}},{{y}_{3}} \right)=\left( x,\dfrac{9-2x}{3} \right) \\
\end{align}\]
\[\therefore \] Centroid of triangle = \[\left( \dfrac{2-2+x}{3},\dfrac{-3+1+\dfrac{9-2x}{3}}{3} \right)\]
Centroid of triangle = \[\left( \dfrac{x}{3},\left( \dfrac{-9+3+9-2x}{9} \right) \right)=\left( \dfrac{x}{3},\dfrac{3-2x}{9} \right)\].
Locus of the centroid = (h, k)
\[\Rightarrow \left( \dfrac{x}{3},\dfrac{3-2x}{9} \right)=\left( h,k \right)\]
Hence from the above, we can say that,
\[h=\dfrac{x}{3}\] and \[k=\dfrac{3-2x}{9}\]
Let us simplify them,
From \[h=\dfrac{x}{3}\], we can say that,
\[\Rightarrow x=3h\]
Now put x = 3h in the expression of k.
\[\begin{align}
  & k=\dfrac{3-2x}{9}=\dfrac{3-2\left( 3h \right)}{9} \\
 & \Rightarrow 9k=3-6h \\
 & \therefore 6h+9k=3 \\
\end{align}\]
Divide the expression throughout by 3.
i.e. 2h + 3k = 1
Now let us replace (h, k) by (x, y). We get,
2x + 3y = 1
Thus we get the locus of the centroid of the triangle as, 2x + 3y = 1.
\[\therefore \] Option (d) is the correct answer.

Note: The centroid is the center of gravity. The centroid should always tie inside the object. It is the point of concurrency of the medians. You can find the centroid of according to the centroid theorem, which states that the centroid of the triangle is at \[{{\dfrac{2}{3}}^{rd}}\] of the distance from the vertex to the mid – point of the sides.