Question

If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC find the length of the median passing through the vertex A.
(a) 5 units
(b) 6 units
(c) 15 units
(d) None of these

Answer 1

Hint: Find the mid-point of straight-line BC, then use distance formula to find the length of median passing through A
Let q be the distance between two points (a, b) and (c, d) is given by:
$q=\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}$

Complete step-by-step answer:
First, we need to find the mid-point of the straight-line BC. For co-ordinates of midpoint, we need the average of the values of $x$ - coordinates and $y$ - coordinates of point B and point C. Let the mid-point be named as D.
Co-ordinates of D = Average of coordinates of B, C
Let $x$ - coordinate of D = p,
       $y$ - coordinate of D =q
From the given points we can say,
$x$ - coordinate of B = 1, $y$ - coordinate of B = - 1
$x$ - coordinate of C = 5, $y$ - coordinate of C = 1
p = Average of $x$ - coordinates of B
\[p=\left( \dfrac{x-\text{coordinate of B + }x\text{ coordinate of C }}{2} \right)\]
By substituting the values, we get:
\[p=\dfrac{5+1}{2}\]
p = 3
Similarly
q = Average of $y$ - coordinates of point B and point C
$q=\dfrac{1+\left( -1 \right)}{2}=\dfrac{1-1}{2}$
q = 0
So, mid-point of line BC = (3, 0)
$\Rightarrow D=\left( 3,0 \right)$

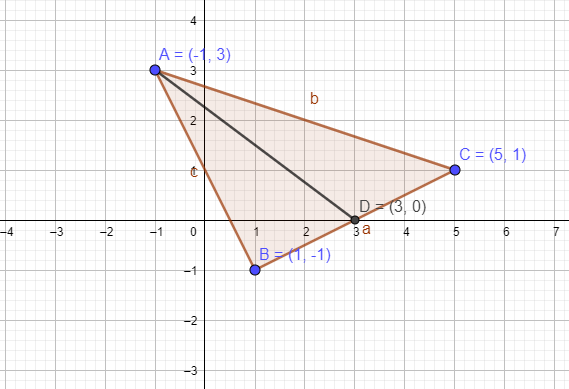
In above figure AD is the median.
Now, we need length of median
A median is a line which passes through a vertex to the mid-point of the side opposite to the particular vertex.
We need the length of the median through the vertex A.
By applying distance formula from the vertex A to the mid-point of side BC, we get length of median
We know, distance formula:
If distance between two points (a, b), (c, d) is q then:
$q=\sqrt{{{\left( c-a \right)}^{2}}+{{\left( d-b \right)}^{2}}}$
Here, we need distance between point A (-1, 3) and the mid-point of side BC: D(3, 0)
From above formula let:
AD = q, a = -1, b = 3, d = 0
By substituting above values in the equation we get
$\begin{align}
  & q=\sqrt{{{\left( 3+1 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}=\sqrt{{{4}^{2}}+{{3}^{2}}} \\
 & q=5 \\
 & \Rightarrow AD=5 \\
\end{align}$
AD is the median through A.
Therefore, the length of the median through A is 5 units.

Note: While calculating the distance formula, take the sign of co-ordinates into consideration. If not, you may lead to the wrong answer.