Question

If A (1, 2), B (-3, 2) and C (3, -2) be the vertices of a \[\Delta ABC\], show that,
(i) $\tan A=2$
(ii) $\tan B=\dfrac{2}{3}$
(iii) $\tan C=\dfrac{4}{7}$

Answer 1

Hint: We will be using the concept of coordinate geometry to solve the problem. We will first using the fact that the angle between two lines with slope ${{m}_{1}},{{m}_{2}}\ is\ \tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$.

Complete step-by-step answer:

Now, we have been given three vertices of a \[\Delta ABC\] are,
A (1, 2), B (-3, 2) and C (3, -2)
So, we have \[\Delta ABC\]as,

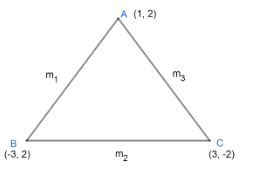
Now, we let the slope $AB={{m}_{1}}$
Also, we know that the slope of line passing through two points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)\ is\ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
${{m}_{1}}=\dfrac{2-2}{-3-1}=0$
Now, let the slope of $BC={{m}_{2}}$
$\begin{align}
  & =\dfrac{2-\left( -2 \right)}{-3-3} \\
 & =\dfrac{2+2}{-6} \\
 & =\dfrac{4}{-6} \\
 & =\dfrac{-2}{3} \\
\end{align}$
Now, let the slope of $AC={{m}_{3}}$
$\begin{align}
  & =\dfrac{2-\left( -2 \right)}{1-3} \\
 & =\dfrac{2+2}{-2} \\
 & =\dfrac{4}{-2} \\
 & =-2 \\
\end{align}$
Now, we know that the angle between two lines having slope ${{m}_{1}},{{m}_{2}}$ is,
$\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$
Now, we know that all the angles in \[\Delta ABC\] are acute. Therefore, tan A, tan B, tan C will be positive only. Therefore, we have,
$\begin{align}
  & \tan A=\left| \dfrac{{{m}_{1}}-{{m}_{3}}}{1+{{m}_{1}}{{m}_{3}}} \right|=\dfrac{0-\left( -2 \right)}{1+\left( 0 \right)\left( -2 \right)} \\
 & \tan A=2 \\
 & \tan B=\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right| \\
 & =\left| \dfrac{0-\left( -\dfrac{2}{3} \right)}{1+\left( 0 \right)\left( -\dfrac{2}{3} \right)} \right| \\
 & =\dfrac{2}{3} \\
\end{align}$
$\begin{align}
  & \tan C=\left| \dfrac{{{m}_{2}}-{{m}_{3}}}{1+{{m}_{2}}{{m}_{3}}} \right| \\
 & =\left| \dfrac{-\dfrac{2}{3}-\left( -2 \right)}{1+\left( -\dfrac{2}{3} \right)\left( -2 \right)} \right| \\
 & =\left| \dfrac{-\dfrac{2}{3}+2}{1+\dfrac{4}{3}} \right| \\
 & =\left| \dfrac{2-\dfrac{2}{3}}{1+\dfrac{4}{3}} \right| \\
 & =\left| \dfrac{\dfrac{6-2}{3}}{\dfrac{3+4}{3}} \right| \\
 & =\dfrac{4}{7} \\
\end{align}$
Therefore, we have showed that,
(i) $\tan A=2$
(ii) $\tan B=\dfrac{2}{3}$
(iii) $\tan C=\dfrac{4}{7}$

Note: To solve these type of question it is important to note that we have used the fact that the angle between two lines with slope ${{m}_{1}},{{m}_{2}}\ is\ \tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$ and the the slope of line passing through two points is $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)\ is\ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.