Question

If (a, 0) is a point on a diameter segment of the circle ${x^2} + {y^2} = 4$, then ${x^2} - 4x - {a^2} = 0$ has:
A.Exactly one real root in $\left( { - 1,0} \right]$
B.Exactly one real root in $\left[ {2,5} \right]$
C.Distinct roots greater than -1
D.Distinct roots less than 5

Answer 1

Hint: We will solve this question by calculating the discriminant of the given quadratic equation ${x^2} - 4x - {a^2} = 0$ and then we will check the value of a by plotting the graph of the circle ${x^2} + {y^2} = 4$ and then, we will determine the nature of the roots.

Complete step-by-step answer:
We are given a circle ${x^2} + {y^2} = 4$ and there is a point (a, 0) on the diameter segment of this circle.
We are required to find the nature of the roots of the quadratic equation ${x^2} - 4x - {a^2} = 0$.
The discriminant of the equation ${x^2} - 4x - {a^2} = 0$is given by $D = {b^2} - 4ac$, where a is the coefficient of ${x^2}$ , b is the coefficient of x and c is the constant term in the equation.
$ \Rightarrow D = {\left( { - 4} \right)^2} - 4\left( 1 \right){\left( { - a} \right)^2} = 16 + 4{a^2}$
Now, we can see that the discriminant of this equation is positive since the square of any number is positive i.e., $16 + 4{a^2} > 0$ and hence, the equation will have real roots.
Now, the sum of the roots of the quadratic equation is $\dfrac{{ - b}}{a}$ = 4, and the product of the roots is given by $\dfrac{c}{a} = \dfrac{{ - {a^2}}}{1} = - {a^2}$. Therefore, we can say that one of the roots is positive and the other is negative.
Now, for the given circle, the radius will be 2 (by comparing it with the standard form of the circle as${x^2} + {y^2} = {r^2}$ ).
The point (a, 0) lies on a diameter segment and hence it can lie at any diameter segment and it is sure that the diameter will pass through origin.
The graph will be:

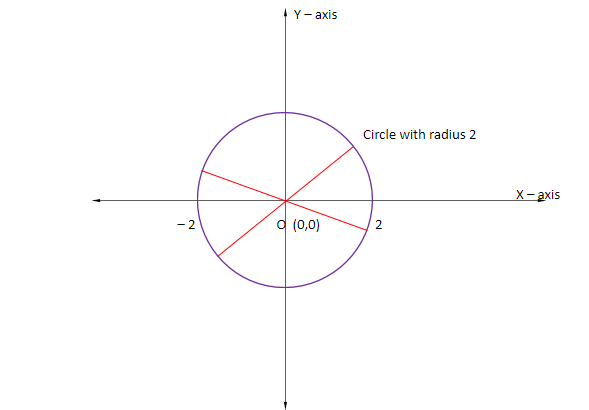
Here, the purple circle is ${x^2} + {y^2} = 4$ with radius 2 and the red line segments represent the diameter segments.
From the graph, we can say that the point (a, 0) will lie on the x – axis at any diameter segment. So, it can take any value from -2 to 2 on the x – axis i.e. $ - 2 \leqslant a \leqslant 2$
Now, checking every option, we get
Option (A): Exactly one real root in $\left( { - 1,0} \right]$
It is correct since the roots are real and one of the roots is negative and also $ - 2 \leqslant a$.
Option (B): Exactly one real root in $\left[ {2,5} \right]$
It is incorrect since the value of a can’t exceed 2.
Option (C): Distinct roots greater than 1
It is incorrect since one of the roots is negative i.e. less than 1.
Option (D): Distinct roots less than 5
It is incorrect since the roots are indeed less than 5 but not for all the values that are less than 5 since $ - 2 \leqslant a \leqslant 2$.
Hence correct option is A.

Note: In this question, you may get confused at many places especially while determining the nature of the roots by the discriminant of the quadratic equation. You may go wrong while verifying the options if they are correct or not. So, calculate everything beforehand in order to avoid observational mistakes.