
If $a$ >\[0\] and \[{{b}^{2}}-4ac\] < \[0\], then the graph of \[y=a{{x}^{2}}+bx+c\]
(a) is concave upwards
(b) is concave downwards
(c) cuts the x-axis
(d) touches the x-axis and lies below it.
Answer
521.1k+ views
Hint: Think of the graph of a quadratic polynomial and play with the coefficients of the quadratic polynomial to determine the nature of the graph.
Complete step by step solution:
The expression given to us is a quadratic polynomial and every quadratic polynomial has a degree \[2\] and the graph of the quadratic polynomial looks like a parabola.
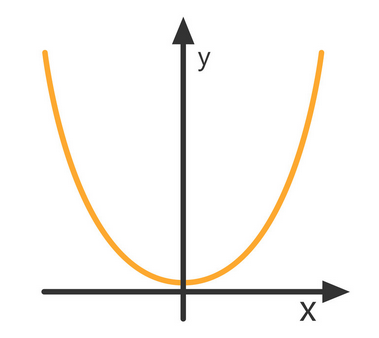
The parabola can open either upwards or downwards. It all depends on the leading coefficient ‘a’. If a>\[0\], the parabola will open upwards and if a<0, the parabola will open downwards.
With the help of this information only, we can answer this question as it is given that a>\[0\] which means the graph will open upwards. Hence the answer should be concave upwards i.e option (a).
The other information which is given to us, \[{{b}^{2}}-4ac\] < \[0\]. It indicates that the graph will not intersect x-axis because \[{{b}^{2}}-4ac\] is the discriminant(D) of this quadratic polynomial and if D<\[0\], it means that both the roots of quadratic equation are imaginary roots and as they are imaginary we cannot plot them on the graph.
The c will be greater than \[0\] because \[{{b}^{2}}-4ac\] < \[0\] which means \[4ac\]>\[{{b}^{2}}\] and we know square of any real number is greater than \[0\]. Therefore, \[{{b}^{2}}\]> \[0\] which further means \[4ac\]> \[0\] and it means both ‘a’ and ‘c’ should have the same sign. And as a>\[0\], c will also be greater than zero.
Note:
From the learnings above, the actual graph of this equation looks like
Complete step by step solution:
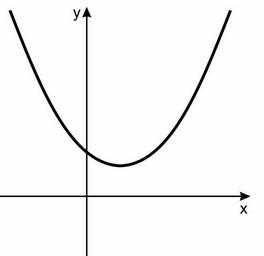
The expression given to us is a quadratic polynomial and every quadratic polynomial has a degree \[2\] and the graph of the quadratic polynomial looks like a parabola.

The parabola can open either upwards or downwards. It all depends on the leading coefficient ‘a’. If a>\[0\], the parabola will open upwards and if a<0, the parabola will open downwards.
With the help of this information only, we can answer this question as it is given that a>\[0\] which means the graph will open upwards. Hence the answer should be concave upwards i.e option (a).
The other information which is given to us, \[{{b}^{2}}-4ac\] < \[0\]. It indicates that the graph will not intersect x-axis because \[{{b}^{2}}-4ac\] is the discriminant(D) of this quadratic polynomial and if D<\[0\], it means that both the roots of quadratic equation are imaginary roots and as they are imaginary we cannot plot them on the graph.
The c will be greater than \[0\] because \[{{b}^{2}}-4ac\] < \[0\] which means \[4ac\]>\[{{b}^{2}}\] and we know square of any real number is greater than \[0\]. Therefore, \[{{b}^{2}}\]> \[0\] which further means \[4ac\]> \[0\] and it means both ‘a’ and ‘c’ should have the same sign. And as a>\[0\], c will also be greater than zero.
Note:
From the learnings above, the actual graph of this equation looks like

Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




