Question

If \[8\operatorname{tanA}=15\], then find \[\sin A-\operatorname{cosA}\].

Answer 1

Hint:First of all we will find the value of \[\sec A\] by using \[1+{{\tan }^{2}}A={{\sec }^{2}}A\]. Now find \[\cos A\] by using \[\cos A=\dfrac{1}{\sec A}\]. Also find \[\sin A\] by using \[si{{n}^{2}}A+{{\cos }^{2}}A=1\]. Now substitute these values in the given expression to get the required answer.

Complete step-by-step answer:
Here, we are given that \[8\operatorname{tanA}=15\] and we have to find the value of \[\sin A-\operatorname{cosA}\].
Let us consider the expression in the question.
\[E=\sin A-\operatorname{cosA}......(1)\]
We are given that \[8\operatorname{tanA}=15\].
So we get \[\operatorname{tanA}=\dfrac{15}{8}\].
We know that \[1+{{\tan }^{2}}A={{\sec }^{2}}A\].
By substituting the value of \[\tan A\], we get as follows:
\[\begin{align}
  & 1+{{\left( \dfrac{15}{8} \right)}^{2}}={{\sec }^{2}}A \\
 & 1+\dfrac{225}{64}={{\sec }^{2}}A \\
 & \dfrac{64+225}{64}={{\sec }^{2}}A \\
 & \dfrac{289}{64}={{\sec }^{2}}A \\
\end{align}\]
So we get \[\sec A=\sqrt{\dfrac{289}{64}}=\dfrac{17}{8}\].
We know that \[\cos A=\dfrac{1}{\sec A}\].
So we get \[\cos A=\dfrac{1}{\dfrac{17}{8}}=\dfrac{8}{17}......(2)\]
We also know that \[si{{n}^{2}}A+{{\cos }^{2}}A=1\].
By substituting the value of \[\operatorname{cosA}=\dfrac{8}{17}\], we get as follows:
\[\begin{align}
  & si{{n}^{2}}A+{{\left( \dfrac{8}{17} \right)}^{2}}=1 \\
 & si{{n}^{2}}A=1-\dfrac{64}{289} \\
 & si{{n}^{2}}A=\dfrac{289-64}{289} \\
 & sinA=\sqrt{\dfrac{225}{289}} \\
 & \sin A=\dfrac{15}{17}......(3) \\
\end{align}\]
Now by substituting \[\sin A=\dfrac{15}{17}\] and \[\operatorname{cosA}=\dfrac{8}{17}\] from equation (3) and equation (2) in equation (1) we get as follows:
\[\begin{align}
  & E=\sin A-\operatorname{cosA} \\
 & E=\dfrac{15}{17}-\dfrac{8}{17} \\
 & E=\dfrac{15-8}{17} \\
 & E=\dfrac{7}{17} \\
\end{align}\]
So we have got the value of \[\sin A-\operatorname{cosA}\] as \[\dfrac{7}{17}\].

Note: Students can also solve this question by considering a triangle ABC as follows:

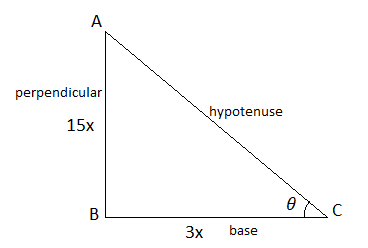
We know that \[\operatorname{tanA}=\dfrac{P}{B}=\dfrac{BC}{AB}=\dfrac{15}{8}\].
So take BC as 15x and AB as 3x and use Pythagoras theorem to find AC as 17x. Now find \[\sin A\] and \[\cos A\] by using \[\dfrac{P}{H}\] and \[\dfrac{B}{H}\] respectively.Substitute the values in the given expression to find the answer.