Question

If 8 is a root of the equation $ {x^2} - 10x + k = 0 $ , then the value of k is-
A. 2
B. 8
C. -8
D. 16

Answer 1

Hint:The concepts of quadratic equations and their roots will be used in the question. The root of a quadratic equation is the value of the variable(x) at which the value of the equation becomes 0. Graphically, it is the point at which the curve of the equation cuts the x-axis. We will substitute the root of the equation and equate it to zero to find the value of k.

Complete step-by-step answer:
A quadratic equation is an equation with a degree of 2. It can have at most 2 real roots, and may sometimes have 1 or none.
We have been given that 8 is a root of the equation $ {x^2} - 10x + k = 0 $ . This implies that this equation has a value of 0 at x = 8. In other words, the graph of the equation cuts the x-axis at x = 8.

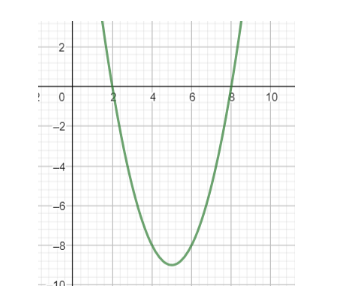
So, we will substitute x = 8 in the given equation, and equate it to zero to find the required value of k. This can be done as-
 $ {\left( 8 \right)^2} - 10\left( 8 \right) + k = 0 $
 $ 64 - 80 + k = 0 $
 $ k - 16 = 0 $
 $ k = 16 $
This is the required value of k. The correct option is D.

Note: A common mistake in such types of problems is that students often confuse the word ‘root’ with the square/cube root. They start finding the square root of the equation, and equate with it 8, which is wrong. They should keep in mind the context in which the word is being used here.