Question

If $5\cot \theta =3$, find the value of \[\left( 5\sin \theta -3\cos \theta \right)\left( 4\sin \theta +3\cos \theta \right)\].

Answer 1

Hint:Divide both sides of the given equation $5\cot \theta =3$ by 5. Assume that in the obtained function: $\cot \theta =\dfrac{3}{5}$, 3 is the length of base and 5 is the length of perpendicular of a right angle triangle. Use Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, to determine the length of the hypotenuse of the right angle triangle. Now find, \[\sin \theta \] by taking the ratio of perpendicular and hypotenuse and $\cos \theta $ by taking the ratio of base and hypotenuse. Now, simplify the expression: \[\left( 5\sin \theta -3\cos \theta \right)\left( 4\sin \theta +3\cos \theta \right)\] by substituting the value of $\sin \theta $ and $\cos \theta $ in the expression to get the answer.

Complete step-by-step answer:

We have been provided with the trigonometric ratio relation: $5\cot \theta =3$. Dividing both sides by 5, we get, $\cot \theta =\dfrac{3}{5}$.
We know that, \[\cot \theta =\dfrac{\text{Base}}{\text{Perpendicular}}\]. Therefore, on comparing it with the above provided ratio, we have, 3 as the length of base and 5 as the length of perpendicular of a right angle triangle.

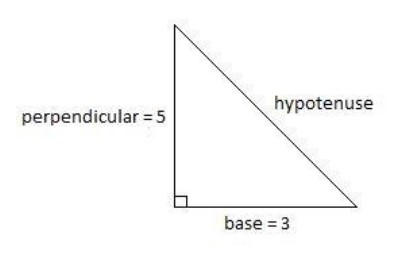
Now, using Pythagoras theorem: $\text{hypotenuse}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicular}{{\text{r}}^{\text{2}}}$, we get,
\[\begin{align}
  & \text{hypotenuse}{{\text{e}}^{\text{2}}}=\text{perpendicular}{{\text{r}}^{\text{2}}}+\text{bas}{{\text{e}}^{\text{2}}} \\
 & \Rightarrow \text{hypotenuse}=\sqrt{\text{perpendicular}{{\text{r}}^{\text{2}}}\text{+bas}{{\text{e}}^{\text{2}}}} \\
 & \Rightarrow \text{hypotenuse}=\sqrt{{{5}^{2}}+{{3}^{\text{2}}}} \\
 & \Rightarrow \text{hypotenuse}=\sqrt{25+9} \\
 & \Rightarrow \text{hypotenuse}=\sqrt{34} \\
\end{align}\]
We know that, \[\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}\].
$\Rightarrow \sin \theta =\dfrac{5}{\sqrt{34}}$
Also, \[\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}\]
$\Rightarrow \cos \theta =\dfrac{3}{\sqrt{34}}$
Here, we have to find the value of the expression: \[\left( 5\sin \theta -3\cos \theta \right)\left( 4\sin \theta +3\cos \theta \right)\].
Now, substituting $\cos \theta =\dfrac{3}{\sqrt{34}}$ and $\sin \theta =\dfrac{5}{\sqrt{34}}$ in the above expression, we get,
\[\begin{align}
  & \left( 5\sin \theta -3\cos \theta \right)\left( 4\sin \theta +3\cos \theta \right) \\
 & =\left( 5\times \dfrac{5}{\sqrt{34}}-3\times \dfrac{3}{\sqrt{34}} \right)\left( 4\times \dfrac{5}{\sqrt{34}}+3\times \dfrac{3}{\sqrt{34}} \right) \\
 & =\left( \dfrac{25}{\sqrt{34}}-\dfrac{9}{\sqrt{34}} \right)\left( \dfrac{20}{\sqrt{34}}+\dfrac{9}{\sqrt{34}} \right) \\
 & =\left( \dfrac{16}{\sqrt{34}} \right)\left( \dfrac{29}{\sqrt{34}} \right) \\
 & =\dfrac{464}{34} \\
 & =\dfrac{232}{17} \\
\end{align}\]

Note: It is important to note that we are dealing with the trigonometry of angles of the first quadrant only, therefore, all the values taken are positive. We can also change the given equation: $5\cot \theta =3$ such that we have to find only one trigonometric ratio. We have to write, $\cot \theta =\dfrac{\cos \theta }{\sin \theta }$ and then by cross-multiplying we will get a relation between \[\sin \theta \] and $\cos \theta $. From there we will substitute the value of either \[\sin \theta \] or $\cos \theta $ in terms of other, in the expression: \[\left( 5\sin \theta -3\cos \theta \right)\left( 4\sin \theta +3\cos \theta \right)\]. Now, the whole expression will be formed in one variable, that is, either \[\sin \theta \] or $\cos \theta $. Now, we have to find the value of only this variable and substitute in the expression.