Question

If $3\cot A=4$, check whether \[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A\] or not.

Answer 1

Hint: It is given that the value of $\cot A=\dfrac{4}{3}$ and we know that $\tan A$ is the reciprocal of $\cot A$ then we can write $\tan A=\dfrac{3}{4}$. Substitute this value of $\tan A$ in \[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}\] then evaluate it. From $\tan A$, find the values of $\sin A\And \cos A$ and then substitute the value of $\sin A$ and $\cos A$ in \[{{\cos }^{2}}A-{{\sin }^{2}}A\]. And then compare the L.H.S and R.H.S of the given equation.

Complete step by step solution:
We are asked to check whether,
\[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A\] is true or not.
It is given that:
$\begin{align}
  & 3\cot A=4 \\
 & \Rightarrow \cot A=\dfrac{4}{3} \\
\end{align}$
From the trigonometry, we know that $\tan A=\dfrac{1}{\cot A}$ so $\tan A=\dfrac{3}{4}$.
Now, we are going to substitute the above calculated value of $\tan A$ in \[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}\].
$\begin{align}
  & \dfrac{1-{{\left( \dfrac{3}{4} \right)}^{2}}}{1+{{\left( \dfrac{3}{4} \right)}^{2}}} \\
 & =\dfrac{1-\dfrac{9}{16}}{1+\dfrac{9}{16}} \\
\end{align}$
$\begin{align}
  & \dfrac{16-9}{16+9} \\
 & =\dfrac{7}{25} \\
\end{align}$
From the above calculated value of $\tan A$ we can determine the value of $\sin A\text{ and }\cos A$.
$\tan A=\dfrac{3}{4}$
To find the value of $\sin A\text{ and }\cos A$ we are drawing a right angled triangle in the below figure.
 

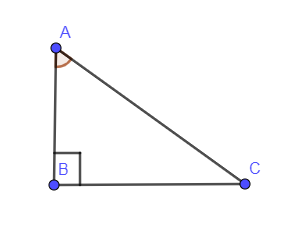
So from Pythagoras theorem we can find the values of $\sin A\text{ and }\cos A$.
And we know that $\tan A=\dfrac{P}{B}$, here “P” stands for perpendicular corresponding to angle A and “B” stands for the base corresponding to angle A.
 $\tan A=\dfrac{3}{4}$
In the above equation, the value of P = 3 and the value of B = 4 so using Pythagoras theorem we can find the hypotenuse using the formula,
$\begin{align}
  & {{H}^{2}}={{P}^{2}}+{{B}^{2}} \\
 & \Rightarrow {{H}^{2}}={{3}^{2}}+{{4}^{2}} \\
 & \Rightarrow {{H}^{2}}=9+16=25 \\
 & \Rightarrow H=5 \\
\end{align}$
From the trigonometric ratios we know that,
$\sin A=\dfrac{P}{H}$
Plugging the values of “P” and “H” in the above equation we get,
$\sin A=\dfrac{3}{5}$
$\cos A=\dfrac{B}{H}$
Plugging the values of “B” and “H” in the above equation we get,
$\cos A=\dfrac{4}{5}$
Substituting the values of $\sin A\text{ and }\cos A$ that we have just derived in \[{{\cos }^{2}}A-{{\sin }^{2}}A\] we get,
$\begin{align}
  & \dfrac{16}{25}-\dfrac{9}{25} \\
 & =\dfrac{7}{25} \\
\end{align}$
From the above calculation we got the value of \[{{\cos }^{2}}A-{{\sin }^{2}}A\] is equal to $\dfrac{7}{25}$.
And we have also calculated above the value of \[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}\] is equal to $\dfrac{7}{25}$.
So, we can say that the equation given in question i.e. \[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A\] is true because both L.H.S and R.H.S of this equation has the same value of $\dfrac{7}{25}$.

Note: The other way of stating the true and false of the statement given in the question is by having a sound understanding of the trigonometric identities.
\[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A\]
In the above equation, if you look carefully at the L.H.S of the equation you will find that it is equal to $\cos 2A$.
\[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\cos 2A\]
And the R.H.S of the given equation is also $\cos 2A$ because:
\[{{\cos }^{2}}A-{{\sin }^{2}}A=\cos 2A\]
As L.H.S = R.H.S so we can say that the statement \[\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A\] is true.
So, there is no need to use this equation $3\cot A=4$.