
If 31z5+51z3 is divisible by 3, where z is a digit less than 5. Values of z are
A.0.1
B.0,3
C.1,3
D.1,4
Answer
577.8k+ views
Hint: Here the sum of numbers given is divisible by 3 so we will Use divisibility test of 3. Because it will help in finding which digits will fit in that place.
Complete step-by-step answer:
Given that ,
31z5+51z3 is divisible by 3.
But the values of digit z are missing.
To find the value of digit z means completing the number.
It is already given that the addition of the numbers is divisible by 3.
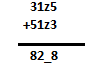
Thus the addition is 82_8. The underscore here represents the sum of z placed digits.
Now, using the divisibility test of 3 we have to find the values of z.
Divisibility test of 3:
If the sum of the digits of the number is exactly divisible by 3 , then the whole number is exactly divisible by 3.
Now , the sum of digits already present is 8+2+8=18.
Since sum is 18 and it is exactly divisible by 3, the sum of z digits should be either 0 or multiple of z .
This simply eliminates option A,C and D. because the sum of those digits is neither 0 nor multiple of 3.
Sum of the digits is 3 and it is multiple of 3 also.
So option B is the correct option..
Note: Using divisibility test will make our work easy.
We can also add the digits of numbers separately and then can find the required value of z.
Complete step-by-step answer:
Given that ,
31z5+51z3 is divisible by 3.
But the values of digit z are missing.
To find the value of digit z means completing the number.
It is already given that the addition of the numbers is divisible by 3.
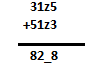
Thus the addition is 82_8. The underscore here represents the sum of z placed digits.
Now, using the divisibility test of 3 we have to find the values of z.
Divisibility test of 3:
If the sum of the digits of the number is exactly divisible by 3 , then the whole number is exactly divisible by 3.
Now , the sum of digits already present is 8+2+8=18.
Since sum is 18 and it is exactly divisible by 3, the sum of z digits should be either 0 or multiple of z .
This simply eliminates option A,C and D. because the sum of those digits is neither 0 nor multiple of 3.
Sum of the digits is 3 and it is multiple of 3 also.
So option B is the correct option..
Note: Using divisibility test will make our work easy.
We can also add the digits of numbers separately and then can find the required value of z.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What are the factors of 100 class 7 maths CBSE

The value of 6 more than 7 is A 1 B 1 C 13 D 13 class 7 maths CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

AIM To prepare stained temporary mount of onion peel class 7 biology CBSE

Write a letter to the editor of the national daily class 7 english CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE





