Question

If \[1c{{m}^{3}}\] of cast iron weights 21 g. Find the weight of the cast iron of length 1m with a bore of 3 cm in which the thickness of the material of the metal is 1 cm.

Answer 1

Hint: We know that if d is the diameter of the circle and r is the radius of the circle, then we get
\[r=\dfrac{d}{2}\]. We know that the difference between outer diameter and inner diameter is equal to thickness of the cast iron. If the length of the object is equal to l, the area of the object is equal to A and volume of the object is equal to V, then \[V=LA\]. By using these concepts, we can find the value of the weight of cast iron.

Complete step by step answer:
From the question, it is given that the bore of the cast iron is equal to 3 cm. We know that the bore is termed as diameter. So, it is clear that the diameter of the cast iron is equal to 3 cm.

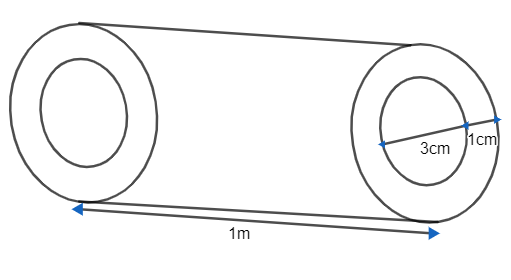
We know that if d is the diameter of the circle and r is the radius of the circle, then we get
\[\Rightarrow r=\dfrac{d}{2}\]
Let us consider
\[r=\dfrac{d}{2}....(1)\]
We know that the diameter of the cast iron is equal to 3 cm. Let us assume the inner radius of the cast iron is equal to \[{{r}_{inside}}\].
\[\begin{align}
  & \Rightarrow {{r}_{inside}}=\dfrac{3}{2} \\
 & \Rightarrow {{r}_{inside}}=1.5...(2) \\
\end{align}\]
From equation (2), it is clear that the value of \[{{r}_{inside}}\] is equal to 1.5 cm.
From the question, we were given that the thickness of the cast iron is equal to 1 cm.
We know that the difference between outer diameter and inner diameter is equal to thickness of the cast iron. Let us assume the value of outer diameter is equal to \[{{r}_{outside}}\].
\[\Rightarrow {{r}_{outside}}-{{r}_{inside}}=1...(3)\]
Now let us substitute equation (2) in equation (3), then we get
\[\begin{align}
  & \Rightarrow {{r}_{outside}}-1.5=1 \\
 & \Rightarrow {{r}_{outside}}=1.5+1 \\
 & \Rightarrow {{r}_{outside}}=2.5...(4) \\
\end{align}\]
From equation (4), it is clear that the value of \[{{r}_{outside}}\] is equal to 2.5 cm.
Now we should find the area of the cast iron. Let us assume the area is equal to A.
\[\Rightarrow A={{A}_{outside}}-{{A}_{inside}}\]
We know that if the radius of the circle is equal to r, then the area of the circle is equal to \[\pi {{r}^{2}}\].
Now we get
\[\begin{align}
  & \Rightarrow A=\pi r_{outside}^{2}-\pi r_{inside}^{2} \\
 & \Rightarrow A=\pi {{\left( 2.5 \right)}^{2}}-\pi {{\left( 1.5 \right)}^{2}} \\
 & \Rightarrow A=6.25\pi -2.25\pi \\
 & \Rightarrow A=4\pi ...(5) \\
\end{align}\]
From equation (5), it is clear that the area of the cast iron is equal to \[4\pi \].
We also know that the volume of an object is equal to the product of area and height.
If the length of the object is equal to l, the area of the object is equal to A and volume of the object is equal to V, then \[V=LA\].
From the question, we were given that the length of the cast iron is equal to 100 cm. Let us assume the volume of the object is equal to V.
\[\Rightarrow V=100A...(6)\]
Now we should substitute equation (6) in equation (5), then we get
\[\begin{align}
  & \Rightarrow V=100\left( 4\pi \right) \\
 & \Rightarrow V=400\pi ....(7) \\
\end{align}\]
From equation (7), it is clear that the volume of cast iron is equal to \[400\pi \].
From the question, it is clear that \[1c{{m}^{3}}\] of cast iron weighs 21 g.
Now we should find the rate of cast iron whose volume of cast iron is equal to \[400\pi c{{m}^{3}}\]. Let us assume the rate of cast iron is equal to R.
\[\begin{align}
  & \Rightarrow R=\left( 400\pi \right)\left( 21 \right) \\
 & \Rightarrow R=26,400g \\
 & \Rightarrow R=26.4kg...(8) \\
\end{align}\]

From equation (8), it is clear that the total weight of cast iron is equal to 26.4 kg.

Note: Students may have a misconception that the sum between outer diameter and inner diameter is equal to thickness of the cast iron. If this misconception is followed, then we cannot get the correct answer. So, students should have a clear view of the concept that the difference between outer diameter and inner diameter is equal to thickness of the cast iron.