Question

If \[0<\beta <\alpha <\dfrac{\pi }{2},\cos (\alpha +\beta )=\dfrac{3}{5}\] and \[\cos (\alpha -\beta )=\dfrac{4}{5}\] , then \[\sin 2\alpha \] is equal to
A. \[0\]
B. \[1\]
C. \[2\]
D. None of these

Answer 1

Hint: To solve this type of problem, we have to observe the conditions given in the questions and then simplify them in the form of alpha and beta. Only after that we have to perform some arithmetic operations and apply some trigonometric identities and we will get our required answer.

Complete step by step answer:
The word trigonometry is derived from the Greek words trigonon (means “triangle”) and metron (means “to measure”).
Trigonometry can be defined as a study of the relationship of angles, lengths and heights.
Inverse trigonometric functions are simply defined as the inverse functions of the basic trigonometric functions which are sine, cosine, tangent, cotangent, secant, and cosecant functions. They are also termed as arcus functions (also called as anti trigonometric functions or cyclometric functions). The inverse of these six trigonometric functions are:
Arcsine, Arccosine, Arctangent, Arcsecant, Arccosecant, Arccotangent.
These are used to find the unknown measure of an angle of a right triangle, and can also be used to find out the value when there is any missing side in a right angle triangle. Trigonometry can also be used to find out the angles of the sound waves and also in the satellites systems and even in the investigation of a crime scene.
As, we are given in the question that: \[\cos (\alpha +\beta )=\dfrac{3}{5}\]
And when we send any trigonometric function to the opposite side of equals to, it becomes the inverse of that.
So,
\[\Rightarrow (\alpha +\beta )={{\cos }^{-1}}\dfrac{3}{5}\]
We are also given: \[\cos (\alpha -\beta )=\dfrac{4}{5}\]

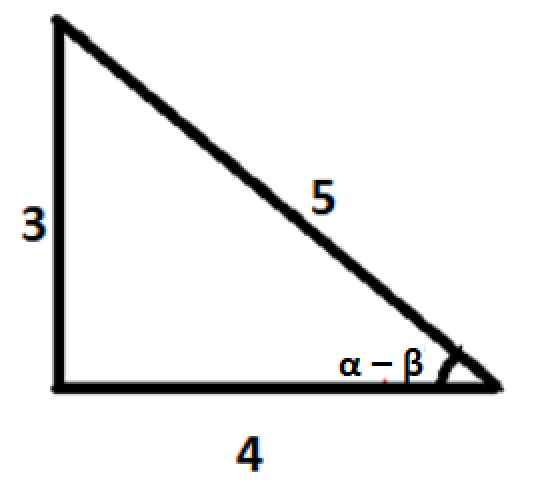
As, from the given triangle we can see that opposite is of \[3\] and hypotenuse is \[5\]
Sine is the ratio of opposite side to the hypotenuse, and cosine is the ratio of adjacent side to the hypotenuse, so we can say that:
\[\cos (\alpha -\beta )=\dfrac{4}{5}\]
\[\Rightarrow \sin (\alpha -\beta )=\dfrac{3}{5}\]
\[\Rightarrow (\alpha -\beta )={{\sin }^{-1}}\dfrac{3}{5}\]
Now, we will add both:
\[(\alpha +\beta )+(\alpha -\beta )={{\cos }^{-1}}\dfrac{3}{5}+{{\sin }^{-1}}\dfrac{3}{5}\]
\[\Rightarrow 2\alpha ={{\cos }^{-1}}\dfrac{3}{5}+{{\sin }^{-1}}\dfrac{3}{5}\]
Now we have to put the values of \[{{\cos }^{-1}}\dfrac{3}{5}\] and \[{{\sin }^{-1}}\dfrac{3}{5}\]
Since, \[{{\sin }^{-1}}\dfrac{3}{5}=36.86\]
And \[{{\cos }^{-1}}\dfrac{3}{5}=53.14\]
Now after putting these values:
\[\Rightarrow 2\alpha =36.86+53.14\]
\[\Rightarrow 2\alpha =90\]
\[\Rightarrow 2\alpha =\dfrac{\pi }{2}\]
Now we will multiply both the sides with sine, it becomes as:
\[\sin 2\alpha =\sin \dfrac{\pi }{2}\]
\[\Rightarrow \sin 2\alpha =1\]
So, the correct answer is “Option B”.

Note: These are used widely in the fields of engineering, physics, geometry and navigation. Using the inverse sine function radius of the sun can be calculated. The captain of the ship can use inverse sine, cosine and tangent function to determine the direction they want to go.