Question

How do you identify the vertical and horizontal translations of sine and cosine from a graph and an equation?

Answer 1

Hint: For the function $$y=f\left(x\right)$$, the vertical translation is described by the equation $$y=f\left(x\right)+a$$ and horizontal translation is described by the equation $$y=f\left(x-a\right)$$. the vertical translation is described by the equation $$y=f\left(x\right)+a$$ such that if $$a$$ is greater than zero then the shift in the graph is upward from the original and if $$a$$ is less than zero then the shift in the graph is downward from the original. the horizontal translation is described by the equation $$y=f\left(x-a\right)$$ such that if $$a$$ is greater than zero then the shift in the graph is toward right from the original and if $$a$$ is less than zero then the shift in the graph is toward left from the original.

Complete step by step solution:
Consider the sine function as $$y=\sin x$$ and the cosine function as $$y=\cos x$$.

It is known that for a function $$y=f\left(x\right)$$, the vertical translation is described by the equation $$y=f\left(x\right)+a$$ such that if $$a$$ is greater than zero then the shift in the graph is upward from the original and if $$a$$ is less than zero then the shift in the graph is downward from the original.

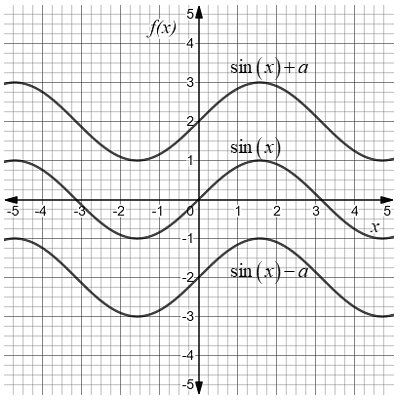
Therefore vertical translation of a sine function is written as $$y=\sin x+a$$ and the vertical translation of a cosine function is written as $$y=\cos x+a$$. Where $$a$$ cannot be zero.

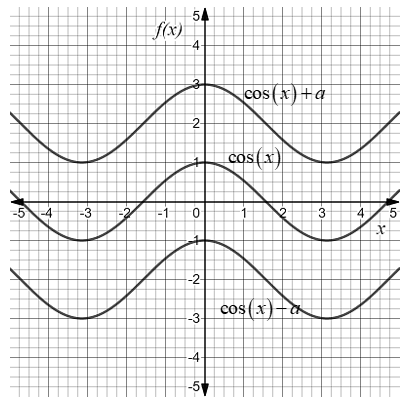
Thus, if we are able to write the sin function in the form $$y=\sin x+a$$ and the cosine function in the form $$y=\cos x+a$$ where in both cases $$a\ne 0$$ then it represents vertical translation in both trigonometric functions from the original.

In the graph, if sine functions or cosine functions wave is not symmetric to $$x$$-axis then there is a vertical shift in the graph from the original.

It is known that for a function $$y=f\left(x\right)$$, the horizontal translation is described by the equation $$y=f\left(x-a\right)$$ such that if $$a$$ is greater than zero then the shift in the graph is toward right from the original and if $$a$$ is less than zero then the shift in the graph is toward left from the original.

Therefore horizontal translation of a sine function is written as $$y=\sin \left(x-a\right)$$ and the horizontal translation of a cosine function is written as $$y=\cos \left(x-a\right)$$. Where $$a$$ cannot be zero.

Thus, if we are able to write the sin function in the form $$y=\sin \left(x-a\right)$$ and the cosine function in the form $$y=\cos \left(x-a\right)$$ where in both cases $$a\ne 0$$ then it represents horizontal translation in both trigonometric functions from the original.

In the graph, if sine functions or cosine functions wave is not symmetric to $$y$$-axis then there is a horizontal shift in the graph from the original.


Note: For horizontal shift, the function is $$y=f\left(x-a\right)$$ and for vertical shift, the function is $$y=f\left(x\right)+a$$ if the original function is $$y=f\left(x\right)$$. The horizontal translation of a sine function is written as $$y=\sin \left(x-a\right)$$ and the horizontal translation of a cosine function is written as $$y=\cos \left(x-a\right)$$. Where $$a$$ cannot be zero. The vertical translation of a sine function is written as $$y=\sin x+a$$ and the vertical translation of a cosine function is written as $$y=\cos x+a$$. Where $$a$$ cannot be zero.