Question

Identify the SSS postulate, based on which the given pair of triangles can be said similar?

Answer 1

Hint:SSS stands for "side, side and side", The SSS postulate states that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent. Which also means that two triangles with all three pairs of corresponding sides lie in the same ratio.
If two triangles have three pairs of sides in the same ratio, then the triangles are similar.

Complete step-by-step answer:
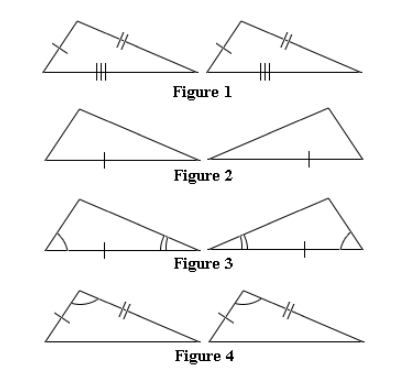
To find which of the following figures follow SSS postulate we should cross check the value of all the sides in the given figures,
Now let us examine the figure 1.
In figure 1 we can see that all the three sides of triangle 1 are equal to the triangle 2.
Hence we have come to a conclusion by SSS postulate that the three sides of one triangle are congruent to three sides of another triangle.
Therefore, both the triangles are congruent to one another.
By congruence and by SSS similarity postulate we can say that the given triangles are similar.
So figure 1 follows SSS postulate.
In figure 3 we can see that two angles and one side are notified therefore we can say that both the triangles are similar by AAS postulate
Whereas in figure 4 we can see that an angle and two sides are notified therefore we can say that both the triangles are similar by SAS postulate
Whereas in figure 2 only one of the sides is notified which is not sufficient to speak about the similarity.

Note:
SSS Similarity Theorem: If all three pairs of corresponding sides of two triangles are proportional, then the two triangles are similar.
The other figures follow SAS, ASA and AAS postulates, Where SAS means “Side Angle Side” postulate, ASA means “Angle Side Angle” postulate, and AAS means “Angle Angle Side” postulate.