Question

Identify the correct statement:
A. If $f\left( x \right)$ is differentiable at $x=a$ , $\left| f\left( x \right) \right|$ will also be differentiable at $x=a$.
B. If $f\left( x \right)$ is continuous at $x=a$ , $\left| f\left( x \right) \right|$ will also be continuous at $x=a$.
C. If $f\left( x \right)$ is discontinuous at $x=a$ , $\left| f\left( x \right) \right|$ will also be discontinuous at $x=a$.
D. If $f\left( x \right)$ is continuous at $x=a$ , $\left| f\left( x \right) \right|$ will also be continuous at $x=a$.

Answer 1

Hint: From the given statements, statement B is correct. Now, here we will check the consciousness of a function according to the following way as:
A function is continuous when its left hand limit, right hand limit and the value at the point exist and are equal to each other i.e.
$ \displaystyle \lim_{x \to {{a}^{-}}}f\left( x \right)=f\left( a \right)=\displaystyle \lim_{x \to {{a}^{+}}}f\left( x \right)$

Complete step by step solution:
Let the $f\left( x \right)$ be a real function and there be a positive number $a$ .
Where, $f\left( x \right)=\left| x \right|$
Since, the modulus function can be defined as:
$\Rightarrow \left\{ \begin{align}
  & f\left( x \right)=x,\text{ if }x>0 \\
 & and \\
 & f\left( x \right)=-x,\text{ if }x<0 \\
\end{align} \right\}$
To find that the modulus function to be continuous at the given point $x=a$ , we will find the value of left hand limit, right hand limit and the value at given point.
Here, we will start from left hand limit that is:
$\Rightarrow f\left( x \right)=-x,\text{ if }x<0$
Now, we will apply the limit at the left hand side of function as:
$\Rightarrow \displaystyle \lim_{x \to {{a}^{-}}}f\left( x \right)$
Now, the above equation will be as:
$\Rightarrow \displaystyle \lim_{x \to {{a}^{-}}}\left( -x \right)$
Since, we already assumed $a$ as a real number. So we can write the above equation i.e. left hand limit as:
$\Rightarrow -\left( -a \right)$
Now, we will open the small bracket in the above equation so that the product of two negative must be positive as:
$\Rightarrow a$
Now, we will solve the right hand limit that is:
$\Rightarrow f\left( x \right)=x,\text{ if }x>0$
We will apply the limit in the right hand side of function as:
$\Rightarrow \displaystyle \lim_{x \to {{a}^{+}}}f\left( x \right)$
Here, the above equation will be as:
$\Rightarrow \displaystyle \lim_{x \to {{a}^{+}}}x$
Since, $a$ is a positive number so that we will get the value from the above equation as:
$\Rightarrow a$
Since, we get the value for left hand limit and right hand limit. Now, we will find the value of the function at a point as:
The function is:
$\Rightarrow f\left( x \right)=\left| x \right|$
Now, after applying $x=a$ , we will have:
$\Rightarrow f\left( a \right)=\left| a \right|$
Since, modulus of a number always gives a positive number and we know that $a$ is a positive number:
$\Rightarrow f\left( a \right)=a$
Hence, we got the equal value from the left hand limit, right hand limit and at the point. Therefore, the modulus function is continuous.

So, the correct answer is “Option B”.

Note: Here, we try to understand the continuity of a modulus function by its graph as:
Since, we have the modulus function as:
$\Rightarrow f\left( x \right)=\left| x \right|$
And it can be derives for negative and positive values as:
$\Rightarrow \left\{ \begin{align}
  & f\left( x \right)=x,\text{ if }x>0 \\
 & and \\
 & f\left( x \right)=-x,\text{ if }x<0 \\
\end{align} \right\}$
And for zero, it will be zero from the value of function at a point that is $0$ here as:
$\Rightarrow f\left( 0 \right)=0$
So, the graph will be as:

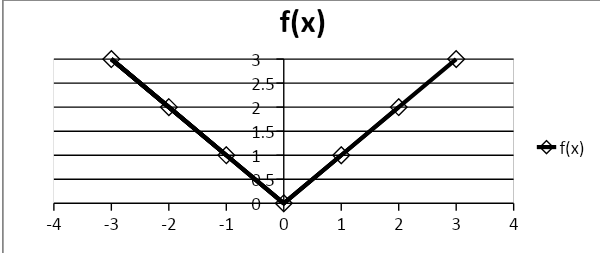
Here, we clearly see that the line is continuous for the domain. Hence, the modulus function is continuous.