
How do you identify if the equation $ {{x}^{2}}=8y $ is a parabola, circle, ellipse, or hyperbola and how do you graph it?
Answer
562.2k+ views
Hint: For answering this question we need to draw the graph of $ {{x}^{2}}=8y $ and we need to verify if the curve is a parabola or circle or ellipse or hyperbola. The equation of the parabola is given as $ {{x}^{2}}=4ay $ where $ a $ is the distance from the vertex to the focus. Similarly the equation of ellipse is given as $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ and hyperbola is $ \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ and similarly circle is $ {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} $ where $ \left( a,b \right) $ is the centre and $ r $ is the radius.
Complete step by step answer:
From the given question it has been asked to find if the equation $ {{x}^{2}}=8y $ is a parabola, circle, ellipse, or hyperbola. From the question, the given equation is, $ {{x}^{2}}=8y $
First of all, let us check whether the equation is parabola or not.
We know that the general form of the equation of the parabola opening up is, $ {{x}^{2}}=4ay $ where,
$ 4 $ in the general form of the equation of the parabola opening up represents “constant”.
$ a $ in the general form of the equation of the parabola opening up represents “the distance from the vertex to the focus”.
Its vertex is $ \left( 0,0 \right) $
The given equation in the question is $ {{x}^{2}}=8y $
It can be rewritten as in the form of, $ {{x}^{2}}=4\times 2\times y $
We can clearly observe that it is in the form of the general form of the equation of the parabola opening up.
It is a parabola opening up with the distance from the vertex to the focus is $ 2 $
Therefore, $ {{x}^{2}}=8y $ represent a parabola.
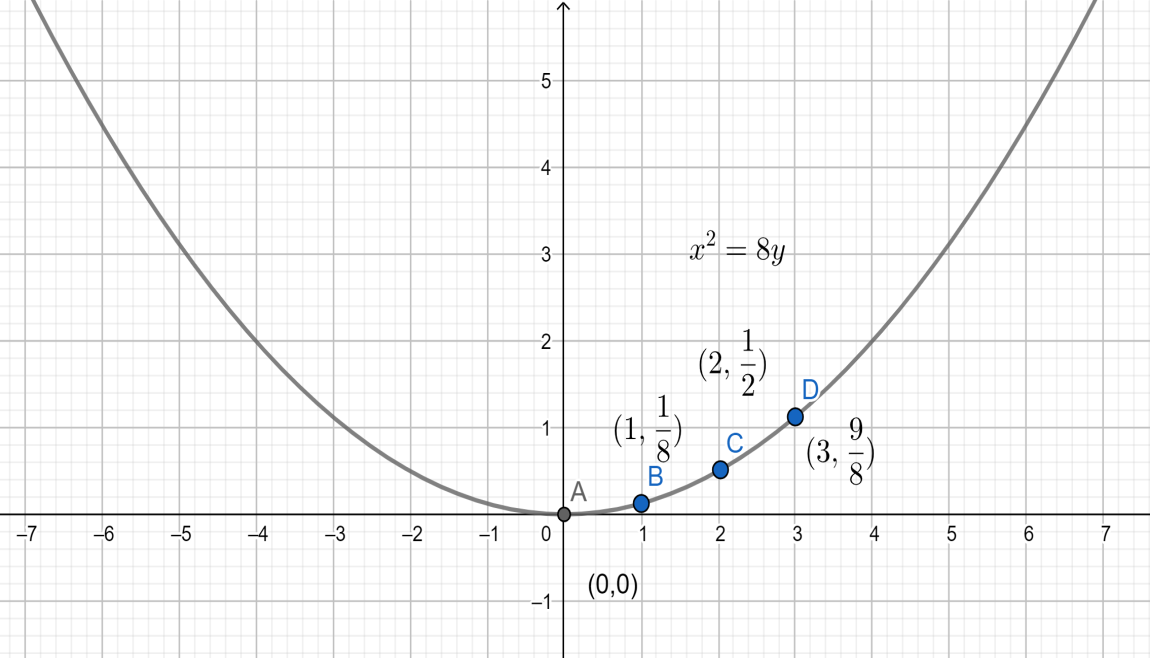
We can graph it as shown in the below graph:
Graphical representation:
Note:
We should be well aware of the general form of the equations of the parabola, ellipse and hyperbola. We should be well aware of the graphical representation of the parabola, ellipse. We should be very careful while doing the calculation. The equation of the parabola is given as $ {{x}^{2}}=4ay $ where $ a $ is the distance from the vertex to the focus. Similarly the equation of ellipse is given as $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ and hyperbola is $ \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ where $ a,b $ are the distances of the major and minor axis and similarly circle is $ {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} $ where $ \left( a,b \right) $ is the centre and $ r $ is the radius.
Complete step by step answer:
From the given question it has been asked to find if the equation $ {{x}^{2}}=8y $ is a parabola, circle, ellipse, or hyperbola. From the question, the given equation is, $ {{x}^{2}}=8y $
First of all, let us check whether the equation is parabola or not.
We know that the general form of the equation of the parabola opening up is, $ {{x}^{2}}=4ay $ where,
$ 4 $ in the general form of the equation of the parabola opening up represents “constant”.
$ a $ in the general form of the equation of the parabola opening up represents “the distance from the vertex to the focus”.
Its vertex is $ \left( 0,0 \right) $
The given equation in the question is $ {{x}^{2}}=8y $
It can be rewritten as in the form of, $ {{x}^{2}}=4\times 2\times y $
We can clearly observe that it is in the form of the general form of the equation of the parabola opening up.
It is a parabola opening up with the distance from the vertex to the focus is $ 2 $
Therefore, $ {{x}^{2}}=8y $ represent a parabola.
We can graph it as shown in the below graph:
| $ x $ | $ y=\dfrac{{{x}^{2}}}{8} $ | $ (x,y) $ |
| 0 | 0 | $ \left( 0,0 \right) $ |
| 1 | $ \dfrac{1}{8} $ | $ \left( 1,\dfrac{1}{8} \right) $ |
| 2 | $ \dfrac{1}{2} $ | $ \left( 2,\dfrac{1}{2} \right) $ |
| 3 | $ \dfrac{9}{8} $ | $ \left( 3,\dfrac{9}{8} \right) $ |
Graphical representation:

Note:
We should be well aware of the general form of the equations of the parabola, ellipse and hyperbola. We should be well aware of the graphical representation of the parabola, ellipse. We should be very careful while doing the calculation. The equation of the parabola is given as $ {{x}^{2}}=4ay $ where $ a $ is the distance from the vertex to the focus. Similarly the equation of ellipse is given as $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ and hyperbola is $ \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ where $ a,b $ are the distances of the major and minor axis and similarly circle is $ {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} $ where $ \left( a,b \right) $ is the centre and $ r $ is the radius.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




