Question

(i) What is the difference in potentials between two points one at $ 10cm $ and other at $ 20cm $ from a charge of $ - 5.5\mu C $
(ii) Which one is at higher potential?

Answer 1

Hint: The question given to us is in two parts, one is to calculate the potential difference between two points and second one is which of those potentials is higher. We can start by drawing a diagram and then finding the potential with help of the formula,
The potential due to the charge at point P is $ {V_P} = \dfrac{{kQ}}{{{r_1}}} $
The potential due to the change at point P’ is $ {V_{P'}} = \dfrac{{kQ}}{{{r_2}}} $
Where $ Q $ is the charge
 $ {r_1} $ and $ {r_2} $ are the distances from the charge to the points.

Complete Step By Step Answer:

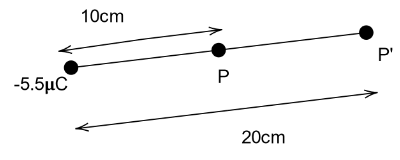
Consider two points P and P’ at distances as shown in the figure.
The difference of potential between the two points P and P’ can be found out using the formula $ {V_P} - {V_{P'}} = \dfrac{{kQ}}{{{r_1}}} - \dfrac{{kQ}}{{{r_2}}} $
Substituting the values, $ {V_P} - {V_{P'}} = \dfrac{{kQ}}{{{r_1}}} - \dfrac{{kQ}}{{{r_2}}} \Rightarrow kQ\left( {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right) = k \times - 5.5 \times \left( {\dfrac{1}{{0.10}} - \dfrac{1}{{0.20}}} \right) $
This can be simplified into $ {V_P} - {V_{P'}} = - 247.5 \times {10^5}V $
(ii) Since the value is negative, the latter value of potential is greater.
That is, $ {V_{P'}} > {V_P} $ .

Note:
Potential difference between two points is defined as the difference in electric potential between two points. Electric potential difference is an important concept in the understanding of electrical circuits.
The formula to find the potential is $ V = k\dfrac{Q}{r} $ .