Question

$I$ is the incenter of $\vartriangle ABC$. If $P$ and $Q$ be the feet of the perpendicular from $A$ to $BI$ and $CI$ , respectively, then \[\dfrac{{AP}}{{BI}} + \dfrac{{AQ}}{{CI}} = \]
A) $\cot \dfrac{A}{2}$
B) $\tan \dfrac{A}{2}$
C) $\sin \dfrac{A}{2}$
D) $\cos \dfrac{A}{2}$

Answer 1

Hint: Incenter is the point of intersection of the bisectors of all the three interior angles of a triangle.

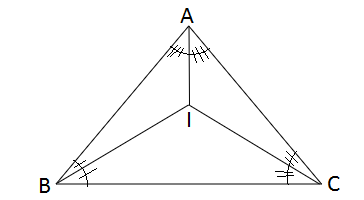
                               Figure: Incenter of a triangle
To draw AP perpendicular to BI, extend the line BI from I. And similarly to draw AQ perpendicular to CI extend the line CI from I.
Use the trigonometric ratio to find the relation between the angles and sides of the triangle.

Complete step-by-step answer:
Step 1: Draw the line AP perpendicular to BI and AQ perpendicular to CI in the given triangle \[\vartriangle ABC\].
$I$ is the incenter of the given triangle \[\vartriangle ABC\].

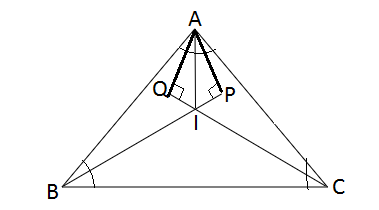
Figure: Given Triangle
In $\vartriangle ABC$, the sum of interior angles is equal to the $180^\circ $or $\pi $.
Thus, $A + B + C = \pi $
Divide by 2 into both sides.
$\dfrac{A}{2} + \dfrac{B}{2} + \dfrac{C}{2} = \dfrac{\pi }{2}$ …… (1)
I is the incenter of the given triangle $\vartriangle ABC$.
Hence, BI is the angle bisector of an angle $B$, likewise, CI is the angle bisector of an angle $C$ and AI is the angle bisector of an angle $A$.
Step 2: Find AP and AQ.
In $\vartriangle ABP$ , $AP \bot BP$.
Hence, $\angle APB = {90^ \circ }$
The sine of an angle is the ratio of perpendicular and hypotenuse.
$\sin \left( {\dfrac{B}{2}} \right) = \dfrac{{AP}}{{AB}}$
$ \Rightarrow AP = AB\sin \left( {\dfrac{B}{2}} \right)$ …… (2)
In $\vartriangle ACQ$ , $AQ \bot CQ$.
Hence, $\angle AQC = {90^ \circ }$
The sine of an angle is the ratio of perpendicular and hypotenuse.
$\sin \left( {\dfrac{C}{2}} \right) = \dfrac{{AQ}}{{AC}}$
$ \Rightarrow AQ = AC\sin \left( {\dfrac{C}{2}} \right)$ …… (3)
Step 3: Find BI and CI using the Sine rule.
The sine rule of a triangle

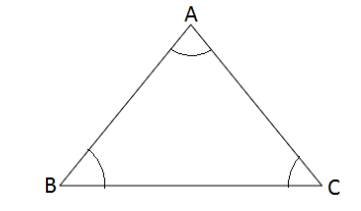
The line segments AB, AC, BC are the opposite side to the angles A, B, and C respectively. Then,
$\dfrac{{AB}}{{\sin C}} = \dfrac{{AC}}{{\sin B}} = \dfrac{{BC}}{{\sin A}}$
In $\vartriangle ABI$, on applying sine rule we have:
$\dfrac{{BI}}{{\sin \dfrac{A}{2}}} = \dfrac{{AB}}{{\sin \left( {\angle AIB} \right)}}$
In $\vartriangle ABI$, the angle sum property of its interior angle, we have,
$
  \dfrac{A}{2} + \dfrac{B}{2} + \angle AIB = \pi \\
   \Rightarrow \angle AIB = \pi - \left( {\dfrac{A}{2} + \dfrac{B}{2}} \right) \\
 $
Applying sine on both sides
$\sin \left( {\angle AIB} \right) = \sin \left[ {\pi - \left( {\dfrac{A}{2} + \dfrac{B}{2}} \right)} \right]$
We know, a trigonometric property $\sin \left( {\pi - x} \right) = \sin x$
Thus, $\sin \left[ {\pi - \left( {\dfrac{A}{2} + \dfrac{B}{2}} \right)} \right] = \sin \left( {\dfrac{A}{2} + \dfrac{B}{2}} \right)$
$ \Rightarrow \sin \left( {\angle AIB} \right) = \sin \left( {\dfrac{A}{2} + \dfrac{B}{2}} \right)$
We have $\dfrac{A}{2} + \dfrac{B}{2} + \dfrac{C}{2} = \dfrac{\pi }{2}$
$\because \dfrac{A}{2} + \dfrac{B}{2} = \dfrac{\pi }{2} - \dfrac{C}{2}$
Thus, $\sin \left( {\dfrac{A}{2} + \dfrac{B}{2}} \right) = \sin \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right)$
$ \Rightarrow \sin \left( {\angle AIB} \right) = \sin \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right)$
We know a trigonometric property $\sin \left( {\dfrac{\pi }{2} - x} \right) = \cos x$
Thus, $\sin \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right) = \cos \dfrac{C}{2}$
$ \Rightarrow \sin \left( {\angle AIB} \right) = \cos \dfrac{C}{2}$
Therefore, $\dfrac{{BI}}{{\sin \dfrac{A}{2}}} = \dfrac{{AB}}{{\cos \dfrac{C}{2}}}$
$ \Rightarrow BI = \dfrac{{AB}}{{\cos \dfrac{C}{2}}}\sin \dfrac{A}{2}$ …… (4)
In $\vartriangle ACI$, on applying sine rule we have:
$\dfrac{{CI}}{{\sin \dfrac{A}{2}}} = \dfrac{{AC}}{{\sin \left( {\angle AIC} \right)}}$
In $\vartriangle ACI$, the angle sum property of its interior angle, we have,
$
  \dfrac{A}{2} + \dfrac{C}{2} + \angle AIC = \pi \\
   \Rightarrow \angle AIC = \pi - \left( {\dfrac{A}{2} + \dfrac{C}{2}} \right) \\
 $
Applying sine on both sides
$\sin \left( {\angle AIC} \right) = \sin \left[ {\pi - \left( {\dfrac{A}{2} + \dfrac{C}{2}} \right)} \right]$
We know, a trigonometric property $\sin \left( {\pi - x} \right) = \sin x$
Thus, $\sin \left[ {\pi - \left( {\dfrac{A}{2} + \dfrac{C}{2}} \right)} \right] = \sin \left( {\dfrac{A}{2} + \dfrac{C}{2}} \right)$
$ \Rightarrow \sin \left( {\angle AIC} \right) = \sin \left( {\dfrac{A}{2} + \dfrac{C}{2}} \right)$
We have $\dfrac{A}{2} + \dfrac{B}{2} + \dfrac{C}{2} = \dfrac{\pi }{2}$
$\because \dfrac{A}{2} + \dfrac{C}{2} = \dfrac{\pi }{2} - \dfrac{B}{2}$
Thus, $\sin \left( {\dfrac{A}{2} + \dfrac{C}{2}} \right) = \sin \left( {\dfrac{\pi }{2} - \dfrac{B}{2}} \right)$
$ \Rightarrow \sin \left( {\angle AIC} \right) = \sin \left( {\dfrac{\pi }{2} - \dfrac{B}{2}} \right)$
We know a trigonometric property $\sin \left( {\dfrac{\pi }{2} - x} \right) = \cos x$
Thus, $\sin \left( {\dfrac{\pi }{2} - \dfrac{B}{2}} \right) = \cos \dfrac{B}{2}$
$ \Rightarrow \sin \left( {\angle AIC} \right) = \cos \dfrac{B}{2}$
Therefore, $\dfrac{{CI}}{{\sin \dfrac{A}{2}}} = \dfrac{{AC}}{{\cos \dfrac{B}{2}}}$
$ \Rightarrow CI = \dfrac{{AC}}{{\cos \dfrac{B}{2}}}\sin \dfrac{A}{2}$ …… (5)
Step 4: Find \[\dfrac{{AP}}{{BI}} + \dfrac{{AQ}}{{CI}}\]
Let's substitute the values of AP, AQ, BI, and CI found in the above calculations.
$
   \Rightarrow \dfrac{{AB\sin \left( {\dfrac{B}{2}} \right)}}{{\dfrac{{AB}}{{\cos \dfrac{C}{2}}}\sin \dfrac{A}{2}}} + \dfrac{{AC\sin \left( {\dfrac{C}{2}} \right)}}{{\dfrac{{AC}}{{\cos \dfrac{B}{2}}}\sin \dfrac{A}{2}}} \\
   \Rightarrow \dfrac{{\sin \left( {\dfrac{B}{2}} \right)\cos \dfrac{C}{2}}}{{\sin \dfrac{A}{2}}} + \dfrac{{\sin \left( {\dfrac{C}{2}} \right)\cos \dfrac{B}{2}}}{{\sin \dfrac{A}{2}}} \\
   \Rightarrow \dfrac{{\sin \left( {\dfrac{B}{2}} \right)\cos \dfrac{C}{2} + \sin \left( {\dfrac{C}{2}} \right)\cos \dfrac{B}{2}}}{{\sin \dfrac{A}{2}}} \\
 $
Using the trigonometric identity: $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$
$ \Rightarrow \dfrac{{\sin \left( {\dfrac{B}{2} + \dfrac{C}{2}} \right)}}{{\sin \dfrac{A}{2}}}$
We have $\dfrac{A}{2} + \dfrac{B}{2} + \dfrac{C}{2} = \dfrac{\pi }{2}$
$\because \dfrac{B}{2} + \dfrac{C}{2} = \dfrac{\pi }{2} - \dfrac{A}{2}$
Thus, $\sin \left( {\dfrac{B}{2} + \dfrac{C}{2}} \right) = \sin \left( {\dfrac{\pi }{2} - \dfrac{A}{2}} \right)$
We know a trigonometric property $\sin \left( {\dfrac{\pi }{2} - x} \right) = \cos x$
Thus, $\sin \left( {\dfrac{\pi }{2} - \dfrac{A}{2}} \right) = \cos \dfrac{A}{2}$
Thus, $\sin \left( {\dfrac{B}{2} + \dfrac{C}{2}} \right) = \cos \dfrac{A}{2}$
$ \Rightarrow \dfrac{{\cos \left( {\dfrac{A}{2}} \right)}}{{\sin \dfrac{A}{2}}}$
We know, \[\cot x = \dfrac{{\cos x}}{{\sin x}}\]
$ \Rightarrow \cot \dfrac{A}{2}$

Final answer: \[\dfrac{{AP}}{{BI}} + \dfrac{{AQ}}{{CI}}\] comes out to be $\cot \dfrac{A}{2}$ . Thus the correct option is (A).

Note: Similarly we have cosine rule of the triangle.

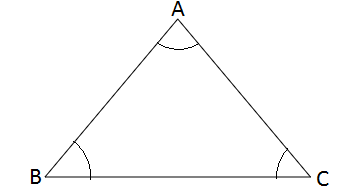
The line segments AB, AC, BC are the opposite side to the angles A, B, and C respectively. Then,
\[{\left( {AB} \right)^2} = {\left( {AC} \right)^2} + {\left( {BC} \right)^2} - 2AC.BC\cos \left( C \right)\]
C is the angle opposite to the side AB.
Properties of Incenter of Triangle:
The incenter of the triangle always lies inside the triangle.
The incenter is the center of the triangle’s incircle, it is the largest circle that lies inside the triangle and touches all the three sides of the triangle.