Question

(i) If the sum of the distances of the point from two perpendicular lines in a plane is 1, then find the locus of the point.
(ii) Find the product of the length of point \[\left( 1,1 \right)\] from the pair of lines \[{{x}^{2}}+xy-6{{y}^{2}}=0\]

Answer 1

Hint: For solving the first part we consider the perpendicular lines as co – ordinate axes. We assume that point as \[P\left( h,k \right)\] and find the distance from this point to co – ordinate axes and use the condition that the sum of distances is 1 to find the locus. The formula for perpendicular distance from point \[A\left( h,k \right)\] to line \[ax+by+0\] is given as
\[D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
For solving the second part we use the factorisation method to find the line equations from the pair of lines then we use the distance formula to each line to find the product.

Complete step by step answer:
First let u solve the first part.
(i) Let us assume that the perpendicular lines as co – ordinate axes.
We know that the equations of Y – axis as
\[\Rightarrow x=0\]
We know that the equation of X – axis as
\[\Rightarrow y=0\]
Let us assume that the arbitrary point as \[P\left( h,k \right)\]
We know that the formula for perpendicular distance from point \[A\left( h,k \right)\] to line \[ax+by+0\] is given as
\[D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
By using the distance formula from \[P\left( h,k \right)\] to Y – axis we get
\[\begin{align}
  & \Rightarrow {{D}_{1}}=\dfrac{\left| h \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\
 & \Rightarrow {{D}_{1}}=\left| h \right| \\
\end{align}\]
By using the distance formula from \[P\left( h,k \right)\] to X – axis we get
\[\begin{align}
  & \Rightarrow {{D}_{2}}=\dfrac{\left| k \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\
 & \Rightarrow {{D}_{2}}=\left| k \right| \\
\end{align}\]
We are given that the sum of distances from point to perpendicular lines as 1
By converting the statement to mathematical equation we get
\[\begin{align}
  & \Rightarrow {{D}_{1}}+{{D}_{2}}=1 \\
 & \Rightarrow \left| h \right|+\left| k \right|=1 \\
\end{align}\]
Here, we can see that there is modulus to each term.
So, we can have four equations after removing the modulus that is
\[\begin{align}
  & \Rightarrow h+k=1 \\
 & \Rightarrow h-k=1 \\
 & \Rightarrow -h+k=1 \\
 & \Rightarrow -h-1=1 \\
\end{align}\]
By combining the all four equations we get the graph as

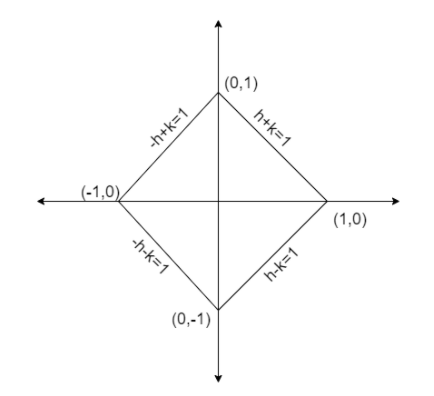
Therefore, we can say that the required locus is a square.
(ii) We are given that the equation of pair of straight lines as
\[\Rightarrow {{x}^{2}}+xy-6{{y}^{2}}=0\]
Let us use the factorisation method to find the equations of straight lines as
\[\begin{align}
  & \Rightarrow {{x}^{2}}+3xy-2xy-6{{y}^{2}}=0 \\
 & \Rightarrow x\left( x+3y \right)-2y\left( x+3y \right)=0 \\
 & \Rightarrow \left( x+3y \right)\left( x-2y \right)=0 \\
\end{align}\]
Here we can see that the equations of straight lines as
\[\Rightarrow x+3y=0.....equation(i)\]
\[\Rightarrow x-2y=0........equation(ii)\]
We are given that the co – ordinate of point as \[A\left( 1,1 \right)\]
Now, by using the distance formula from \[A\left( 1,1 \right)\] to equation (i) we get the distance as
\[\begin{align}
  & \Rightarrow {{D}_{1}}=\dfrac{\left| 1+3 \right|}{\sqrt{{{1}^{2}}+{{3}^{2}}}} \\
 & \Rightarrow {{D}_{1}}=\dfrac{4}{\sqrt{10}} \\
\end{align}\]
Similarly, by using the distance formula from \[A\left( 1,1 \right)\] to equation (ii) we get the distance as
\[\begin{align}
  & \Rightarrow {{D}_{2}}=\dfrac{\left| 1-2 \right|}{\sqrt{{{1}^{1}}+{{2}^{2}}}} \\
 & \Rightarrow {{D}_{2}}=\dfrac{1}{\sqrt{5}} \\
\end{align}\]
We are asked to find the product of length.
Let us assume that the product of length as \[P\] them=n we get
\[\begin{align}
  & \Rightarrow P={{D}_{1}}\times {{D}_{2}} \\
 & \Rightarrow P=\dfrac{4}{\sqrt{10}}\times \dfrac{1}{\sqrt{5}} \\
\end{align}\]
By replacing the value \[\sqrt{10}=\sqrt{5}\times \sqrt{2}\] we get
\[\Rightarrow P=\dfrac{4}{5\sqrt{2}}\]
Therefore the product of length of point \[\left( 1,1 \right)\] from the pair of lines \[{{x}^{2}}+xy-6{{y}^{2}}=0\]is \[\dfrac{4}{5\sqrt{2}}\]

Note: Students may make mistakes in the distance formula.
 We know that the formula for perpendicular distance from point \[A\left( h,k \right)\] to line \[ax+by+0\] is given as
\[D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Students may miss the modulus in the above formula which results in a wrong answer.
In the first part we have the locus as
\[\Rightarrow \left| h \right|+\left| k \right|=1\]
It represents the square.
If the modulus is not taken then the locus will be straight line which is the wrong answer.