Question

(I) Derive expression for angle of banking.
(ii) Derive the relation between \[v\] and \[\omega \]

Answer 1

Hint: (i) Banking turn is a turn or change in direction in which vehicle inclined, usually towards the inside of the turn and the banking angle is the angle at which the vehicle is inclined about its longitudinal axis with respect to the horizontal.
(ii)The rate of change of displacement is known as velocity and The rate of change of angular displacement is known as angular velocity.

Complete step by step answer: (i) Consider a vehicle of mass ‘m’ which is moving with a speed of ‘\[v\] ’ on the banked road with radius ‘\[r\] ’. Let θ be the angle of banking. Here \[f\] is the frictional force that is acting between the road and tyres of the vehicles.

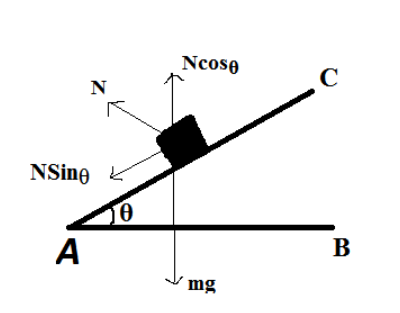
Now, total upwards force will be equal to total downwards force which is acting on the vehicle.
\[N\operatorname{Cos} \theta = mg + f\operatorname{Sin} \theta \]
Where, \[N\operatorname{Cos} \theta \] is the component of normal reaction (as shown in the figure)
\[mg\] is the weight of the vehicle, which is acting in downward direction(as shown)
\[f\operatorname{Sin} \theta \] is the component of frictional force(acting along the vertical axis)
So, \[mg = N\operatorname{Cos} \theta - f\operatorname{Sin} \theta \] ----------- (1)
\[\dfrac{{m{v^2}}}{r} = N\operatorname{Sin} \theta + f\operatorname{Cos} \theta \] ---------- (2)
Here, \[N\operatorname{Sin} \theta \] is the component of normal reaction along the horizontal axis.
\[f\operatorname{Cos} \theta \] is the component of frictional force(acting along the horizontal axis)
Now, divide equation (1) and (2)
\[\dfrac{{\dfrac{{m{v^2}}}{r}}}{{mg}} = \dfrac{{N\operatorname{Sin} \theta + f\operatorname{Cos} \theta }}{{N\operatorname{Cos} \theta - f\operatorname{Sin} \theta }}\]
\[\Rightarrow \dfrac{{{v^2}}}{{rg}} = \dfrac{{N\operatorname{Sin} \theta + f\operatorname{Cos} \theta }}{{N\operatorname{Cos} \theta - f\operatorname{Sin} \theta }}\]
We know, \[f = {\mu _s}N\]
Here, \[f\]is the frictional force.
Now, substitute the value of frictional force in the resultant equation.
\[\dfrac{{{v^2}}}{{rg}} = \dfrac{{N\operatorname{Sin} \theta + {\mu _s}N\operatorname{Cos} \theta }}{{N\operatorname{Cos} \theta - {\mu _s}N\operatorname{Sin} \theta }}\]
\[\dfrac{{{v^2}}}{{rg}} = \dfrac{{\operatorname{Sin} \theta + {\mu _s}\operatorname{Cos} \theta }}{{\operatorname{Cos} \theta - {\mu _s}\operatorname{Sin} \theta }}\]
Now, divide by \[\operatorname{Cos} \theta \] on the right hand side,
We get- \[\dfrac{{{v^2}}}{{rg}} = \dfrac{{\left( {\tan \theta + {\mu _s}} \right)}}{{\left( {1 - {\mu _s}\tan \theta } \right)}}\]
So, \[v = \sqrt {\dfrac{{rg\left( {\tan \theta + {\mu _s}} \right)}}{{\left( {1 - {\mu _s}\tan \theta } \right)}}} \]
\[\Rightarrow {v_{\max }} = \sqrt {rg\operatorname{Tan} \theta } \]
\[\operatorname{Tan} \theta = \dfrac{{{v^2}}}{{rg}}\]
So, \[\theta = {\operatorname{Tan} ^{ - 1}}\dfrac{{{v^2}}}{{rg}}\]
Here θ is known as the angle of Banking.

(ii) Consider a body P is moving along the circumference of a circle of radius r with linear velocity\[v\] and angular velocity \[\omega \].

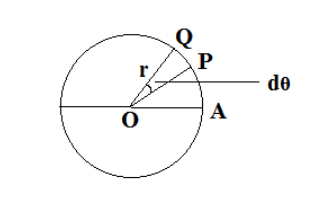
Let's say it is moving from point P to Q in time \[dt\]and \[d\theta \] be the angle swept by the radius vector.
Let PQ is the arc length of the particle moving along the circle\[ = ds\]
So, angular displacement\[ = d\theta = \dfrac{{ds}}{r}\]
According to the definition of velocity,\[ds = vdt\]
Put the value of \[ds\]in angular displacement,
We get- \[\dfrac{{d\theta }}{{dt}} = \dfrac{v}{r}\]
\[
  \omega = \dfrac{v}{r} \\
  \Rightarrow v = \omega r \\
 \]
Here, \[\omega \] is the angular velocity.
Thus for a given angular velocity \[\omega \], the linear velocity \[v\] of any particle is directly proportional to the distance of the particle from the centre of the circular path.

Note: (i)The angle of banking depends on the speed of vehicle, radius of the curved road and the acceleration due to gravity at that place. It is independent of mass.
(ii) If a body is moving in uniform circular motion then the angular velocity is the same for all the points but the linear velocity will be different for different points of the body.