Question

I am solving trigonometry, I have an upcoming question for word problems, how do I know if it is a trigonometric ratio word problem, or cosine/sine law word problem?

Answer 1

Hint:
According to the question, first we need to understand the terms. Then we will figure out how to categorize which word problem is a trigonometric ratio word problem and which is s sine or cosine law word problem.

Complete step by step solution:
In Mathematics, trigonometry is said to be a study about the relationship between the sides and the angles of a right-angled triangle.
Trigonometric ratios are the ratios of the sides of a right-angle triangle. In trigonometry, there are three basic trigonometric ratios. They are \[{\text{sine, cosine, tangent}}\]. We have a short form for all the three. They are \[\sin ,\,\cos ,\,\tan \]respectively. These trigonometric ratios are also known as trigonometric functions. With the help of these trigonometric ratios we can calculate or find the angles and sides of a triangle. But trigonometric ratios work only for the right-angled triangles and not for any other type of triangles.
The sine and the cosine rules are different. These rules or laws can be used for any type of triangles. When we want to find the sides and angles of a triangle we mean that we are solving a triangle.
The sine law says that it can be used when either of the two are given (i) one side and two angles, or (ii) an angle which is not being included and two sides.
If we see a triangle \[ABC\] in the figure shown. Let us assume that \[A\] is the angle at \[A\] and \[B\] is the angle at \[B\]. Then, \[a = BC\], \[b = AC\], \[c = AB\].

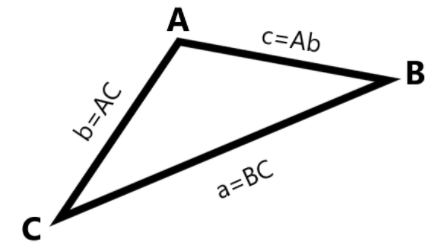
The sine rule says that:
\[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}\]
The cosine law says that it can be used when either of the two are given (i) three sides are given (ii) the angle which is included is given and two sides.
If we see the figure shown is a triangle \[ABC\].

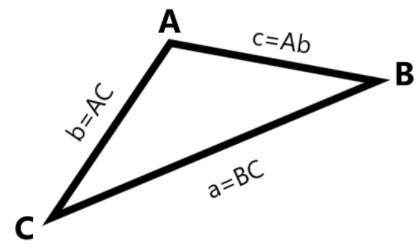
The cosine law says that:
\[{a^2} = {b^2} + {c^2} - 2bc\cos A\]
\[{b^2} = {a^2} + {c^2} - 2ac\cos B\]
\[{c^2} = {a^2} + {b^2} - 2ab\cos C\]

Note:
When you see that you have no angles given and there are three sides given. Then, you should use the cosine law. In every triangle, when you are finding the angles of a triangle, then you should always check whether all the angles sum up to \[{180^ \circ }\].