Question

What is the hypotenuse angle congruence theorem?

Answer 1

Hint: Two triangles are congruent when the two triangles are identical; every side and every angle are equal between the triangles. This theorem is also known as HA theorem. We have to use the application of ASA congruence theorem.

Complete step by step solution:
Hypotenuse angle congruence theorem states that if the hypotenuse and an acute angle of the right triangle are congruent to the hypotenuse and an acute angle of another triangle, then two triangles are said to be congruent.
Let us consider two right angled triangles \[\Delta ABC\] and \[\Delta XYZ\].

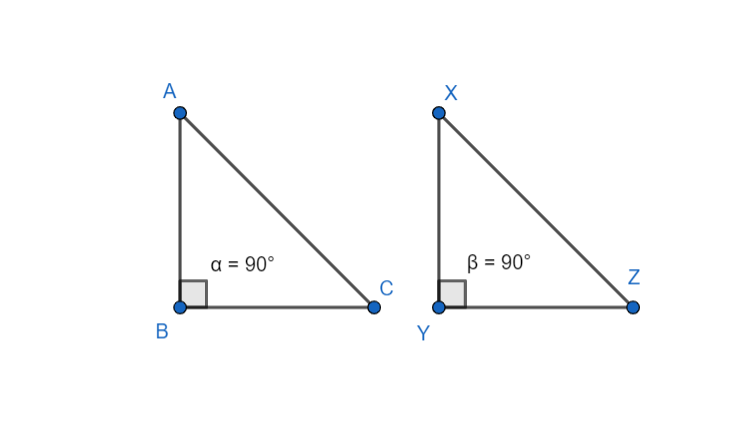
We know that \[\angle B\] and \[\angle Y\] are right angles and \[AC\] and \[XZ\] are hypotenuse of the right triangles respectively.
we are told that the hypotenuse, \[AC\] and \[XZ\] are congruent. We are also told that \[\angle A\] and
\[\angle X\] are congruent.
Looking carefully, \[\angle A\] and \[\angle B\] are consecutive angles in \[\Delta ABC\]. Those two angles do not include a known side between them.
 \[\angle C\] and \[\angle Z\] must be congruent because we said earlier. When two angles are given, the third side is found by subtracting the given two angles from \[{{180}^{0}}\].
In\[\Delta ABC\]
\[\Rightarrow \angle A+\angle B+\angle C={{180}^{0}}\]
\[\Rightarrow \angle A+{{90}^{0}}+\angle C={{180}^{0}}\]
\[\Rightarrow \angle C={{90}^{0}}-\angle A\]
In\[\Delta XYZ\]
\[\Rightarrow \angle X+\angle Y+\angle Z={{180}^{0}}\]
\[\Rightarrow \angle X+{{90}^{0}}+\angle Z={{180}^{0}}\]
\[\Rightarrow \angle Z={{90}^{0}}-\angle X\]
We know that \[\angle A\] and \[\angle X\] are congruent. If we subtract these angles from \[{{180}^{0}}\] we will get the remaining angle congruent (I.e \[\angle C\] and \[\angle Z\]).
So, \[\angle C\] and \[\angle Z\] are congruent.
Now we know that all three angles are congruent and we know that the included side between angles are congruent, now we have ASA postulated.
ASA postulate tells us that triangles are congruent if any two angles and their included side are equal in the triangles.
\[\angle B\cong \angle Y\] (two right angles which we used to deduce \[\angle C\cong \angle Z\])
\[\angle A\cong \angle X\]
Hypotenuse \[AC\]= hypotenuse \[XZ\]
\[\angle C\cong \angle Z\] (deduced from \[\angle A\cong \angle X\] and \[\angle B\cong \angle Y\]).
Hence, we have proved the hypotenuse angle congruence theorem.

Note: Students should use proper ASA congruence theorems. We should know some basic properties of right angle triangles. also, some basic congruence rules. To do this type of question students have to be strong in concepts. Misconception may lead to this question wrong.