Question

How will you construct a ${150}^o$ angle?

Answer 1

Hint: In this particular question use the concept that 150 degree is the bisector of the angle 120 and the angle 180 degree, so first draw 120 and 180 degrees and then draw the bisector of these angles so use these concepts to reach the solution of the question.

Complete step-by-step answer:
The steps of the construction are given below:
$\left(i\right)$ First draw a horizontal line AB of some appropriate distance as shown below.

$\left(ii\right)$ Now draw a semicircle from any point (O) on the line AB with some appropriate radius less than AB, which cuts the line AB at C and D as shown in the below figure.

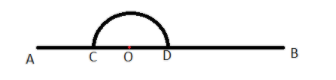
$\left(iii\right)$ Now with same radius mark the arc on the semicircle from point D which cuts the semicircle at point E, now again with same radius mark the arc on the semicircle from point E which cuts the semicircle at point F as shown below.

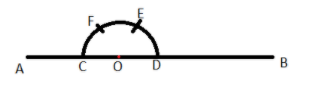
$\left(iv\right)$ Now make an arc from point F with some appropriate distance and again with same distance mark an arc from point C which cuts the previous arc at point G as shown below, then join the points O and G as shown below

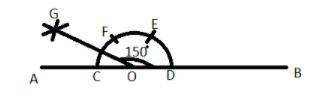
So angle GOB is the required ${150}^o$ angle.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the above written steps. These steps are the basis of the construction without knowing these steps we cannot draw the 150 degree angle and do not skip any steps while constructing.