
How many times does $18$ go into $60?$
Answer
542.1k+ views
Hint: Read the question twice which states that $60$ divided by $18$. Here we will first frame the given expression and then divide to find the remainder and the resultant required value.
Complete step-by-step solution:
To find the number of $18$which can go in $60$, it can be known by
$\dfrac{{60}}{{18}}$
Start division –
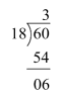
Hence, $18$ can go maximum three times and $6$will be left over.
It can be expressed as: $3\dfrac{6}{{18}}$
Common factors from the numerator and the denominator cancel each other.
$3\dfrac{6}{{18}} = 3\dfrac{1}{3}$
This is the required solution.
Alternative method:
The above problem can be solved by using the multiples method.
First just note down the multiples of the divisor that is $18$
Multiples of $18$ are $18,36,54$
There can be only three multiples of $18$which are less than $60$
Subtract last multiple from $60$
Which gives $6$ left over and hence can be expressed as $3\dfrac{6}{{18}}$
Common factors from the numerator and the denominator cancel each other.
$3\dfrac{6}{{18}} = 3\dfrac{1}{3}$
This is the required solution.
Additional Information: Prime factorization is the process of finding which prime numbers can be multiplied together to make the original number, where prime numbers are the numbers greater than $1$ and which are not the product of any two smaller natural numbers. For Example: $2,{\text{ 3, 5, 7,}}......$ $2$ is the prime number as it can have only $1$ factor. Factors are the number $1$and the number itself.
Note: Be good in multiples and division. Since it is the most important fundamental to solve and simplify any mathematical expression. Remember multiples till twenty numbers. Always convert the given number in the prime numbers and then find the common factors in the numerator and the denominator and then remove them.
Complete step-by-step solution:
To find the number of $18$which can go in $60$, it can be known by
$\dfrac{{60}}{{18}}$
Start division –
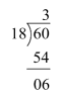
Hence, $18$ can go maximum three times and $6$will be left over.
It can be expressed as: $3\dfrac{6}{{18}}$
Common factors from the numerator and the denominator cancel each other.
$3\dfrac{6}{{18}} = 3\dfrac{1}{3}$
This is the required solution.
Alternative method:
The above problem can be solved by using the multiples method.
First just note down the multiples of the divisor that is $18$
Multiples of $18$ are $18,36,54$
There can be only three multiples of $18$which are less than $60$
Subtract last multiple from $60$
Which gives $6$ left over and hence can be expressed as $3\dfrac{6}{{18}}$
Common factors from the numerator and the denominator cancel each other.
$3\dfrac{6}{{18}} = 3\dfrac{1}{3}$
This is the required solution.
Additional Information: Prime factorization is the process of finding which prime numbers can be multiplied together to make the original number, where prime numbers are the numbers greater than $1$ and which are not the product of any two smaller natural numbers. For Example: $2,{\text{ 3, 5, 7,}}......$ $2$ is the prime number as it can have only $1$ factor. Factors are the number $1$and the number itself.
Note: Be good in multiples and division. Since it is the most important fundamental to solve and simplify any mathematical expression. Remember multiples till twenty numbers. Always convert the given number in the prime numbers and then find the common factors in the numerator and the denominator and then remove them.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




