Question

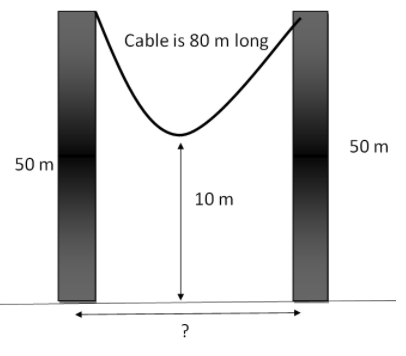
How far apart are the Poles?

Answer 1

Hint:
Here we need to solve the problem in which the distance between the poles which is connected by cable of 80 m long to two poles, and height of each pole is 50 m and distance between cable and the surface is 10 m is given as follows. We will use the catenary equation to solve this problem. We will use this height and distance to solve the equation. From there, we will get the distance between the poles.

Complete step by step solution:
Here we need to find the distance between these poles. As this cable is catenary in shape.
So, we will use the catenary equation to solve it.
Now, we will redraw the figure with \[x\]-axis and \[y\]-axis and represent the height as one of the points of the catenary.

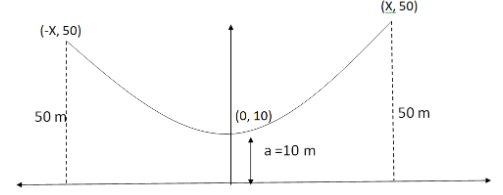
We know the equation of the catenary.
\[y = a\cosh \left( {\dfrac{x}{a}} \right)\]
Here we have \[a = 10\] as it is the lowest point of the catenary.
We will substitute this value in the equation of the catenary.
\[ \Rightarrow y = 10\cosh \left( {\dfrac{x}{{10}}} \right)\]
We know from the figure, one point which lies on the catenary is \[\left( {x,50} \right)\] . So, it will satisfy the equation of the catenary.
Substituting \[y = 50\] in the above equation, we get.
 \[ \Rightarrow 50 = 10\cosh \left( {\dfrac{x}{{10}}} \right)\]
Dividing 10 on both sides, we get
\[\begin{array}{l} \Rightarrow \dfrac{{50}}{{10}} = \cosh \left( {\dfrac{x}{{10}}} \right)\\ \Rightarrow 5 = \cosh \left( {\dfrac{x}{{10}}} \right)\end{array}\]
Now, from the tables of hyperbolic cosine function, we got
\[ \Rightarrow 2.3 = \dfrac{x}{{10}}\]
Multiplying 10 on both sides, we get
\[ \Rightarrow 2.3 \times 10 = x\]
Multiplying the numbers, we got
\[ \Rightarrow x = 23\]
We know distance of the pole is equal to \[2x\]
Therefore,
Distance between the poles \[ = 2x = 2 \times 23 = 46\]

Thus the distance between the poles is equal to 46 m.

Note:
Here we have used the catenary equation to solve this problem. The catenary is defined as a curve which is two dimensional or a plane curve and its shape looks like a hanging chain.
The equation of catenary is given by \[y = a\cosh \left( {\dfrac{x}{a}} \right)\].
Here, we might make a mistake by thinking the distances between the poles is 80 m because the length of the cable is 80m. This will be wrong because the cable is loosely hanging between the poles and not tightly connected. If it would have been tightly connected to the poles then the distance might be the same as the length of the cable.