Question

How does \[\sin x=0\] equals \[\pi \]?

Answer 1

Hint: In this problem, we have to find how \[\sin x=0\] equals \[\pi \]. We should always know that the sine value is always equal to zero for every multiple of \[\pi \], where \[\pi \] radians is equal to \[{{180}^{\circ }}\]. We can now draw a graph with a sine curve to see the value of sine for \[\pi \].

Complete step by step answer:
We know that the given trigonometric function given is sine.
We should always remember that the sine value is always equal to zero for every multiple of \[\pi \], where \[\pi \] radians is equal to \[{{180}^{\circ }}\].
We can now draw a graph with a sine curve to see the value of sine for \[\pi \].

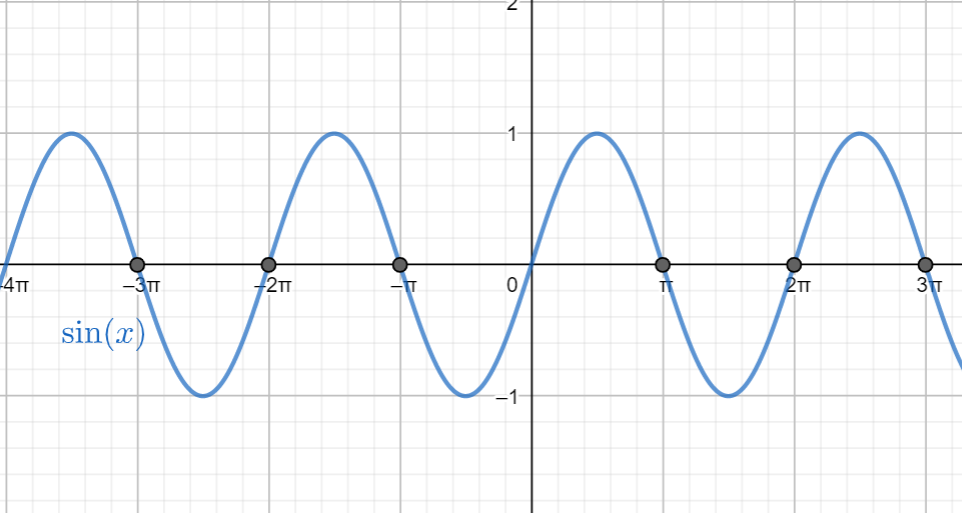
We can now see that the sine curve touches the line at 0 in every multiple of \[\pi \].
We can now write it as,
\[\Rightarrow \sin x=0\to x=k\times \pi \]
Where k is any whole number.
Therefore, we can summarize that every multiple of \[\pi \] for the sine function is always equal to zero.

Note: Students should also remember that \[\pi \] radians is equal to \[{{180}^{\circ }}\]. We should also know that the sine function goes from 0 to \[{{90}^{\circ }}=\dfrac{\pi }{2}\]and then back to 0 to \[{{180}^{\circ }}=\pi \], and when we come down to -1 to \[{{270}^{\circ }}=\dfrac{3\pi }{2}\] and when we go up to 0 again at \[{{360}^{\circ }}=2\pi \], therefore, it will be 0 at every multiple of \[\pi \]. We should also concentrate in the graph part while drawing the sine curve.