Question

How do you solve \[y = 2x - {x^2}\] graphically?

Answer 1

Hint: We know that the given equation is of parabola. So we know how to plot it but here the case is we need to plot the given function anything it is graphically. So we will take different values of x and by putting that value in the equation we will find the values of y. This will be repeated and we will get at least four such pairs. And then we will plot the graph of the equation so given.

Complete step-by-step answer:
Given that equation to be plotted is,
\[y = 2x - {x^2}\]
Now we will take this equation as \[f\left( x \right) = y = 2x - {x^2}\]
Now we will find the value of function for different values of x.
x=-1
\[f\left( { - 1} \right) = 2\left( { - 1} \right) - {\left( { - 1} \right)^2} = - 2 - 1 = - 3\]
That is the value of y is -3.
x=0
\[f\left( 0 \right) = 2\left( 0 \right) - {\left( 0 \right)^2} = 0\]
That is the value of y is 0.
x=1
\[f\left( 1 \right) = 2\left( 1 \right) - {\left( 1 \right)^2} = 2 - 1 = 1\]
That is the value of y is 1.
x=2
\[f\left( 2 \right) = 2\left( 2 \right) - {\left( 2 \right)^2} = 4 - 4 = 0\]
That is the value of y is 0.
Now the pairs \[\left( { - 1, - 3} \right),\left( {0,0} \right),\left( {1,1} \right)\& \left( {2,0} \right)\] are to be plotted on the graph so that it will be the graphical solution.

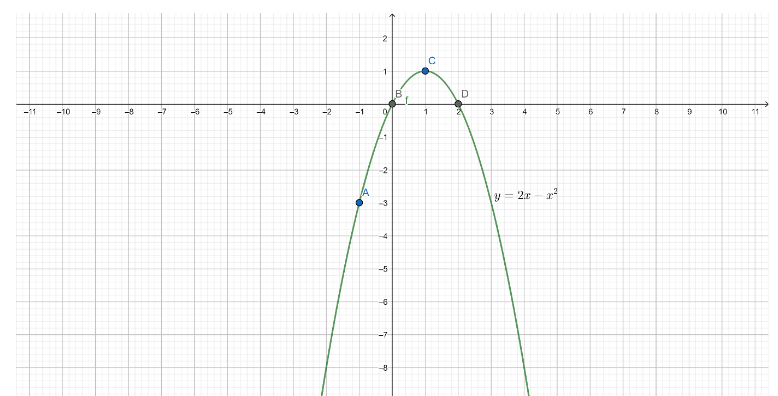
Note: Here note that if the question is not mentioned with the method to be followed we will need to find the vertex, focus, directrix and other such parameters related to the parabolic equation. and need to know which opening parabola is that.