Question

How do you solve ${x^{\dfrac{1}{2}}} = 5$?

Answer 1

Hint: First, move 5 to the left side of the equation by subtracting it from both sides. Then, add 5 to both sides of the equation. Next, raise each side of the equation to the 2 power to eliminate the fractional exponent on the left side. Then, apply the power rule and multiply exponents, ${\left( {{a^m}} \right)^n} = {a^{mn}}$. Next, Multiply the exponents of $x$, i.e., rewrite ${x^{\dfrac{1}{2} \times 2}}$ as $x$. Finally, raise 5 to the power of 2 to get the desired result.
Formula used:
i). Power rule to combine exponents: ${a^m} \times {a^n} = {a^{m + n}}$
ii). $\sqrt[n]{{{a^x}}} = {a^{\dfrac{x}{n}}}$
iii). ${\left( {{a^m}} \right)^n} = {a^{mn}}$

Complete step-by-step solution:
Given: ${x^{\dfrac{1}{2}}} = 5$
Move 5 to the left side of the equation by subtracting it from both sides.
${x^{\dfrac{1}{2}}} - 5 = 0$
Add 5 to both sides of the equation.
${x^{\dfrac{1}{2}}} = 5$
Raise each side of the equation to the 2 power to eliminate the fractional exponent on the left side.
${\left( {{x^{\dfrac{1}{2}}}} \right)^2} = {5^2}$
Apply the power rule and multiply exponents, ${\left( {{a^m}} \right)^n} = {a^{mn}}$.
${x^{\dfrac{1}{2} \times 2}} = {5^2}$
Multiply the exponents of $x$, i.e., rewrite ${x^{\dfrac{1}{2} \times 2}}$ as $x$.
${x^1} = {5^2}$
It can be written as
$x = {5^2}$
Now, raise 5 to the power of 2 to simplify it further.
$x = 25$
Therefore, $x = 25$ is the solution of ${x^{\dfrac{1}{2}}} = 5$.

Note: We can check our solution by plotting the graph of ${x^{\dfrac{1}{2}}} = 5$.
Graph of ${x^{\dfrac{1}{2}}} = 5$:

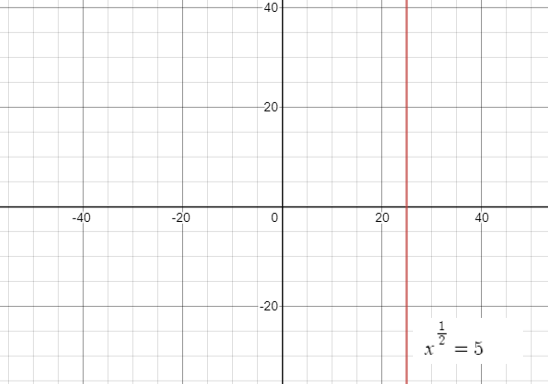
From the graph, we can clearly see that $x = 25$ is the only solution of ${x^{\dfrac{1}{2}}} = 5$.
Final solution: Therefore, $x = 25$ is the solution of ${x^{\dfrac{1}{2}}} = 5$.
Remember that when $a$ is a positive real number, both of these equations are true:
${x^{ - a}} = \dfrac{1}{{{x^a}}}$
$\dfrac{1}{{{x^{ - a}}}} = {x^a}$
The rule for fractional exponents:
When you have a fractional exponent, the numerator is the power and the denominator is the root. In the variable example ${x^{\dfrac{a}{b}}}$​​​​, where $a$ and $b$ are positive real numbers and $x$ is a real number, $a$ is the power and $b$ is the root.
${x^{\dfrac{a}{b}}} = \sqrt[b]{{{x^a}}}$