Question

How do you solve \[x-7y=13\] for \[y\]?

Answer 1

Hint: In order to solve the question, we firstly simplify the equation by keeping all the terms containing \[y\] on the left side and all the other terms on the right. Then, the value of y is found in terms of variable \[x\] and the constant.

Complete step-by-step solution:
First of all, let us simplify the equation as given:
\[x-7y=13\]
Keeping the terms containing \[y\]on the left side and all the other terms on the right
\[-7y=13-x\]
Now, dividing the equation by \[-7\]on both the sides,
\[\begin{align}
  & \Rightarrow y=\dfrac{-13}{7}-\dfrac{x}{-7} \\
 & \Rightarrow y=\dfrac{-13}{7}+\dfrac{x}{7} \\
 & \Rightarrow y=\dfrac{x}{7}-\dfrac{13}{7} \\
\end{align}\]
Here, if we see in this equation, that it is the equation for a straight line,
The slope for the equation
\[\begin{align}
  & m=\dfrac{1}{7} \\
 & x-intercept\Rightarrow \\
\end{align}\]
Putting, \[y=0\]
\[\begin{align}
  & \Rightarrow 0=\dfrac{x}{7}-\dfrac{13}{7} \\
 & \Rightarrow x=13 \\
\end{align}\]
And for \[y-intercept\]\[\Rightarrow \]
Putting,\[x=0\], we get
\[y=-\dfrac{13}{7}\]
If we plot this graph, we get a straight line as:

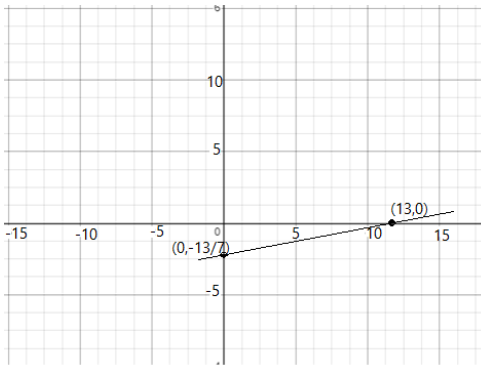
Note: The straight line obtained in the graph gives the slope equal to \[\dfrac{1}{7}\]for the straight line graph, and the intercepts
\[\begin{align}
  & x=13 \\
 & y=-\dfrac{13}{7} \\
\end{align}\]