Question

How do you solve $\sin 2x=\dfrac{1}{2}$?

Answer 1

Hint: The trigonometric function sine is equal to the ratio of the opposite side to the hypotenuse side of the angle. Due to the change in sign of the opposite side in the various quadrants, the sine value may be positive or negative.

Complete Step by Step Solution:
The given trigonometric equation is $\sin 2x=\dfrac{1}{2}$. It contains only one trigonometric function $\sin 2x$ and so there is no need for simplification. We can directly find out the unknown variable.
$\Rightarrow \sin 2x=\dfrac{1}{2}$
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{1}{2} \right)=2x$
The sine function gives a positive value only in the range of angles in between ${{0}^{\circ }}$ and ${{180}^{\circ }}$. In other words, it is positive in the first and second quadrants only. This is because the value of the opposite side is positive only in these quadrants.

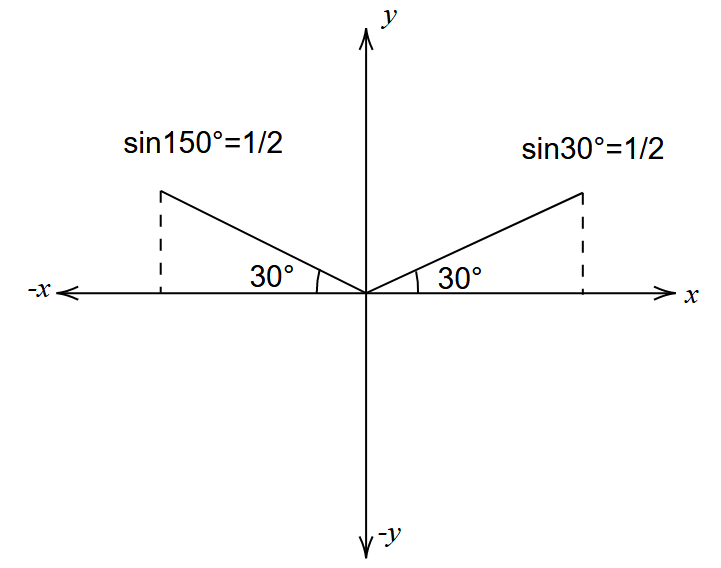
The sine function will be equal to $\dfrac{1}{2}$ at ${{30}^{\circ }}$ or $\dfrac{\pi }{6}$ radians and at ${{150}^{\circ }}$ or $\dfrac{5\pi }{6}$ radians.
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{1}{2} \right)=2x=\dfrac{\pi }{6},\dfrac{5\pi }{6}$
$\Rightarrow x=\dfrac{\pi }{12},\text{ }\dfrac{5\pi }{12}$
Since sine is a periodic function with a period equal to $2\pi $ radians, the variable x will be equal to
$\Rightarrow x=\dfrac{\pi }{12}+2\pi n,\text{ }\dfrac{5\pi }{12}+2\pi n$ where n is an integer.

Note:
It is important to know the sign of the trigonometric ratios in all four quadrants. This will help us to sort out the position of the point in the coordinate system. In addition to that, we should consider the periodicity property of these trigonometric functions and we should include the period of the particular function in the final result.