Question

How do you solve ${\sec ^2}x - 2{\tan ^2}x = 0$?

Answer 1

Hint: First, we have to simplify the given equation using trigonometry identities. Then, take the square root on both sides of the equation. Next, find the values of $x$ satisfying $\tan \left( x \right) = 1$ by taking the inverse tan of both sides of the equation to extract $x$ from inside the tan. Next, find the value of $x$ satisfying $\tan \left( x \right) = - 1$ using trigonometric properties. Then, we will get all solutions of the given equation.
Formula used:
${\sec ^2}\theta = {\tan ^2}\theta + 1$
$\tan \dfrac{\pi }{4} = 1$
$\tan \left( {\pi - x} \right) = - \tan x$
$\tan \left( {2\pi - x} \right) = - \tan x$

Complete step by step solution:
Given equation: ${\sec ^2}x - 2{\tan ^2}x = 0$
We have to find all possible values of $x$ satisfying a given equation.
First, use identity ${\sec ^2}\theta = {\tan ^2}\theta + 1$ in the above equation.
${\tan ^2}x + 1 - 2{\tan ^2}x = 0$
$ \Rightarrow {\tan ^2}x = 1$
Take the square root on both sides of the equation.
$ \Rightarrow \tan x = \pm 1$
Now, we will find the values of $x$ satisfying $\tan \left( x \right) = 1$.
So, take the inverse tan of both sides of the equation to extract $x$ from inside the tan.
$x = \arctan \left( 1 \right)$
Since, the exact value of $\arctan \left( 1 \right) = \dfrac{\pi }{4}$.
$ \Rightarrow x = \dfrac{\pi }{4}$
Since, the tan function is positive in the first and third quadrants.
So, to find the second solution, add the reference angle from $\pi $ to find the solution in the fourth quadrant.
$x = \pi + \dfrac{\pi }{4}$
$ \Rightarrow x = \dfrac{{5\pi }}{4}$
Since, the period of the $\tan \left( x \right)$ function is $\pi $ so values will repeat every $\pi $ radians in both directions.
$x = \dfrac{\pi }{4} + n\pi ,\dfrac{{5\pi }}{4} + n\pi $, for any integer $n$.
Now, we will find the values of $x$ satisfying $\tan \left( x \right) = - 1$…(i)
So, using the property $\tan \left( {\pi - x} \right) = - \tan x$ and $\tan \dfrac{\pi }{4} = 1$ in equation (i).
$ \Rightarrow \tan \left( x \right) = - \tan \dfrac{\pi }{4}$
$ \Rightarrow \tan \left( x \right) = \tan \left( {\pi - \dfrac{\pi }{4}} \right)$
$ \Rightarrow x = \dfrac{{3\pi }}{4}$
Now, using the property $\tan \left( {2\pi - x} \right) = - \tan x$ and $\tan \dfrac{\pi }{4} = 1$ in equation (i).
$ \Rightarrow \tan \left( x \right) = - \tan \dfrac{\pi }{4}$
$ \Rightarrow \tan \left( x \right) = \tan \left( {2\pi - \dfrac{\pi }{4}} \right)$
$ \Rightarrow x = \dfrac{{7\pi }}{4}$
Since, the period of the $\tan \left( x \right)$ function is $\pi $ so values will repeat every $\pi $ radians in both directions.
$x = \dfrac{{3\pi }}{4} + n\pi ,\dfrac{{7\pi }}{4} + n\pi $, for any integer $n$.
Final solution: Hence, $x = \dfrac{\pi }{4} + n\pi ,\dfrac{{3\pi }}{4} + n\pi ,\dfrac{{5\pi }}{4} + n\pi ,\dfrac{{7\pi }}{4} + n\pi $, for any integer $n$ are solutions of the given equation.

Note:
 In the above question, we can find the solutions of a given equation by plotting the equation, ${\sec ^2}x - 2{\tan ^2}x = 0$ on graph paper and determine all its solutions.

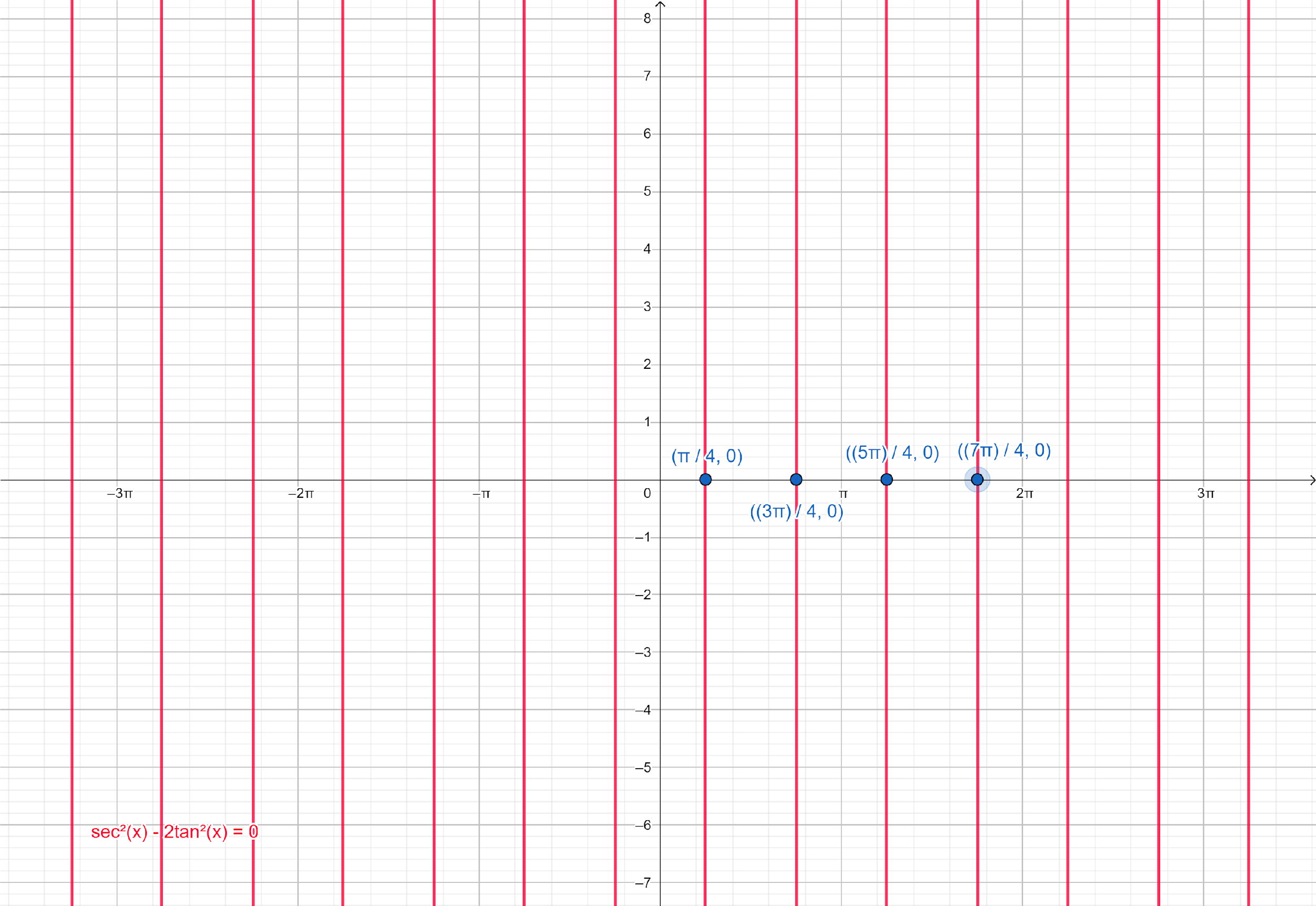
From the graph paper, we can see that $x = \dfrac{\pi }{4}$, $x = \dfrac{{3\pi }}{4}$, $x = \dfrac{{5\pi }}{4}$ and $x = \dfrac{{7\pi }}{4}$ are solution of given equation, and solution repeat every $\pi $ radians in both directions.
So, these will be the solutions of the given equation.
Final solution: Hence, $x = \dfrac{\pi }{4} + n\pi ,\dfrac{{3\pi }}{4} + n\pi ,\dfrac{{5\pi }}{4} + n\pi ,\dfrac{{7\pi }}{4} + n\pi $, for any integer $n$are solutions of the given equation.