Question

How do you solve $\left| -2x+8 \right|<20$?

Answer 1

Hint: Since the absolute value is given, consider both the positive and the negative value of the term inside the absolute value. First take $+\left( -2x+8 \right)<20$ and find the value of ‘x’. then take $-\left( -2x+8 \right)<20$ and find the value of ‘x’. From these two values find the range of ‘x’.

Complete step by step solution:
The equation we have $\left| -2x+8 \right|<20$
As we know, the absolute value of ‘a’ has two values i.e. $\left| a \right|=\pm a$
So, the absolute value of $\left| -2x+8 \right|=\pm \left( -2x+8 \right)$
We have to consider both the values for the solution of the given equation.
First taking $+\left( -2x+8 \right)<20$, we get
$\begin{align}
  & \Rightarrow -2x+8<20 \\
 & \Rightarrow -2x<20-8 \\
 & \Rightarrow -x<\dfrac{12}{2} \\
 & \Rightarrow -x<6 \\
\end{align}$
Again as we know if a < b, then $-a > -b$ (since the direction of the sign changes when we multiply with a negative number)
So it can be written as
$\Rightarrow x >-6$
Then taking $-\left( -2x+8 \right) < 20$, we get
$\begin{align}
  & \Rightarrow 2x-8<20 \\
 & \Rightarrow 2x<20+8 \\
 & \Rightarrow x<\dfrac{28}{2} \\
 & \Rightarrow x<14 \\
\end{align}$
Hence, the solution of $\left| -2x+8 \right|<20$ is $x\in \left( -6,14 \right)$
This is the required solution of the given question.

Note: When we multiply or divide a negative number in both the sides of an inequality then the ‘greater than (>)’ sign changes to ‘less than (<)’ and vice-versa. The obtained result can be verified by plotting the given function on graph as follows

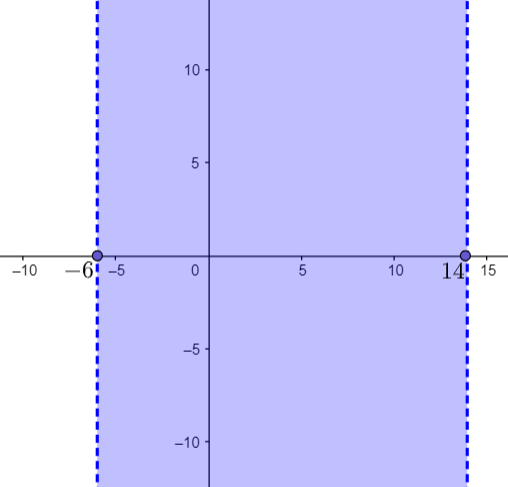
From the above graph, we can conclude that ‘x’ is greater than $-6$ and less than 14.